Factors And Multiples

If a is divisible by b, then b is a factor of a, and a is a multiple of b. For example, 30 = 3 × 10, so 3 and 10 are factors of 30 and 30 is a multiple of 3 and 10

Take note that 1 is a factor of every number.

Understanding factors and multiples is essential for solving many math problems.

Prime Factors

A factor which is a prime number is called a prime factor. For example, the prime factorization of 180 is 2 × 2 × 3 × 3 × 5

You can use repeated division by prime numbers to obtain the prime factors of a given number.

The following diagram shows how to find the GCF using the Ladder Method. Scroll down the page for more examples and solutions.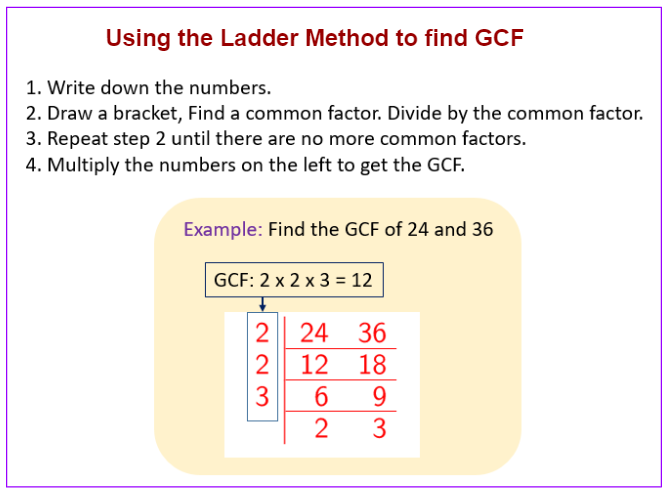

 

Greatest Common Factor (GCF)

As the name implies, we need to list the factors and find the greatest one that is common to all the numbers. For example, to get the GCF of 24, 60 and 66:

The factors of 24 are 1, 2, 3, 4, 6, 8, 12 and 24 The factors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 and 60

The factors of 66 are 1, 2, 3, 6, 11, 22,33 and 66

Look for the greatest factor that is common to all three numbers – thus 6 is the GCF of 24, 60 and 66.

Least Common Multiple (LCM)

As the name implies, we need to list the multiples and to find the least one that is common to all the numbers. For example, to get the LCM of 3, 6 and 9:

The multiples of 3 are 3, 6, 9, 12, 15, 18, 21 … The multiples of 6 are 6, 12, 18, 24, …

The multiples of 9 are 9, 18, 27, …

Look for the least multiple that is common to all three numbers – thus 18 is the LCM of 3, 6 and 9.

Shortcut To Finding LCM
Here is a useful shortcut (also called the ladder method) to finding the LCM of a set of numbers. For example, to find the LCM of 3, 6 and 9, we divide them by any factor of the numbers in the following manner:

How to use the Ladder method to find GCF, LCM and simplifying fractions?
Step 1: Write the two numbers on one line.
Step 2: Draw the L shape.
Step 3: Divide out common prime numbers starting with the smallest.
LCM makes an L.
GCF is down the left side.
Simplified fraction is on the bottom.
Example:
Find the GCF, LCM and simplified fraction for 24 and 36.

LCM & GCF With the Ladder Method
Example:
Find the LCM and GCF of 24 and 36.

Difference between greatest common factor and least common multiple
Example: Find the GCF and LCM of 16 and 24.

Prime Factorization using Factor Trees

These lessons, with videos, examples, and solutions, help students learn how to use a factor tree to find the prime factors of given numbers.

Every composite number can be expressed as a product of prime factors. This product is called the prime factorization of the number. We can use a factor tree to find the prime factors.

Example:
Find the prime factorization of 36.

Solution:

 

The prime factors of 36 are 2 and 3.

We can write 36 as a product of prime factors: 2 × 2 × 3 × 3

The factor tree method is quite flexible – at each branch you can break the number into any factors until you reach the prime factors.
 

The result is the same: 36 = 3 × 2 × 2 × 3

Although the order of the factors may be different because we can start with different pairs of factors, every factor tree of 36 has the same prime factorization.

We can also use exponents to write the prime factorization.

36 = 2² × 3²

Review prime and composite numbers
A prime number natural number greater than 1 that only has two factors: one and itself.
Examples: 2,3,5,7,11,13,17,19, …

A composite number is a natural number that has more than two factors.
The number 1 is neither prime nor composite.

Prime Factorization
To determine the prime factorization of a natural number, we need to find the prime numbers that when multiplied together gives us the original number.
We need to be careful not to confuse prime factorization with the factors of a number. The factors of a number are any two numbers whose product give the original number. Factors do not need to be prime.

We can find the prime factorization of a number using the factor tree.

Example:
Determine the prime factorization of the following numbers:

1. 24
2. 54
3. 120
4. 625

Prime Factorization Using Repeated Division

In these lessons, we will learn how to find prime factors using factor trees and repeated division.

What Are Prime Factors

The prime factors of a number are factors which are prime numbers. We can find the prime factors of a number by repetitive division or stacked division. To find the prime factorization of the number, we need to find the prime factors that when multiplied together gives the number.

Example:
Find the prime factors of 36.
The following diagrams show Prime Factorization of a number using Factors Trees and using Repeated Division. Scroll down the page for more examples and solutions of prime factorization.

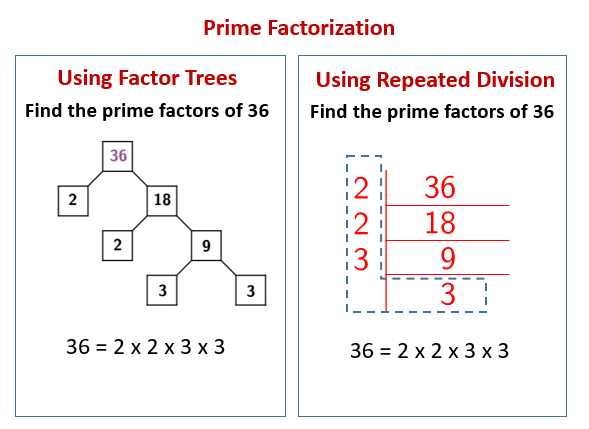
The prime factors of 36 are 2 and 3.

We can write 36 as a product of prime factors: 2 × 2 × 3 × 3

To find prime factors using the repetitive division, it is advisable to start with a small prime factor and continue the process with bigger prime factors.

Prime Factorization Using Stacked Division

Examples of how to use stacked division to find the prime factorization of a number rather than making a prime factorization tree.

Helpful Divisibility Rules
A number is divisible by 2 if it is even or ends in 0, 2, 4, 6, 8.
A number is divisible by 3 if the sum of the digits is divisible by 3.
A number is divisible by 5 if it ends in 0 or 5.

Example:
Use division to find the prime factorization.
a) 300
b) 693

Prime Factorization Using Stacked Division

Example:
Use division to find the prime factorization of 6,552.

Prime Factorization with Upside Down Division

Prime factors of a number can be found by using upside down division.

Prime Factorization with Upside Down Division

Example:
Find the prime factorization of the 210 by the division method.

Examples of prime factorization using repeated division

6, 24, 35, 51