In these lessons, we will learn how to round whole numbers to the nearest ten, hundred and thousand.
Sometimes, we do not need to work with very accurate numbers. For example, suppose that the attendance at a football match was 26,239. Most people may just want to know there were 26,000 at the football match instead of the exact number.
We can round off large numbers to the nearest thousand, nearest hundred, nearest ten, or any other specified place value.
Rounding Numbers To The Nearest Ten
Example:
Round 378 to the nearest ten.
Solution: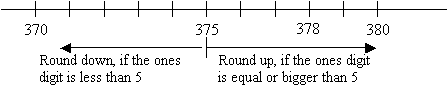
To round off to the nearest ten, we look at the ones digit.
In the number 378, the ones digit is bigger than 5, so we round up to 380.
378 is 380 when rounded off to the nearest ten.
Remember:
The rule is – if the digit to the right of the rounding place is:
5 or more, round up
4 or less, round down
Example:
1 653 is 1 650 when rounded off to the nearest ten.
53 745 is 53 750 when rounded off to the nearest ten.
How to round numbers to the nearest 10?
If the digit in the ones place is:
5 or higher, round tens place up
4 or lower, leave tens place as is
Digits in other places does not matter.
Example:
Round the following numbers to the nearest 10
738
293
197
Rounding Whole Numbers: Round to the Nearest Ten
- Locate the digit one place to the right of the digit in the indicated rounding place.
- If it is 5 or more, round up by 1. If it is 4 or less do not change.
- Change all digits to the right of the rounding place digit to zeros.
Example:
Round the following to the nearest ten.
a) 63
b) 77
c) 85
Rounding Numbers To The Nearest Hundred
Example:
Round 1 243 to the nearest hundred.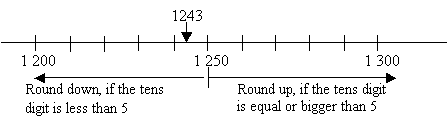
Solution:
To round off to the nearest hundred, we look at the tens digit.
In the number 1 243, the tens digit is less than 5, so we round down to 1 200.
1 243 is 1 200 when rounded off to the nearest hundred.
Examples:
37 084 is 37 100 when rounded off to the nearest hundred.
54 253 is 54 300 when rounded off to the nearest hundred.
Round 3-digit Numbers to the Nearest Hundred
Use a number line to understand rounding to the nearest hundred.
Rounding Whole Numbers: Round To The Nearest Hundred
Example:
Round to the nearest hundred
a) 1,839
b) 22,386
Rounding Numbers To The Nearest Thousand
Example:
Round 46 225 to the nearest thousand.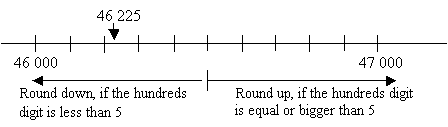
Solution:
To round off to the nearest thousand, we look at the hundreds digit.
In the number 46 225, the hundreds digit is less than 5, so we round down to 46 000.
46 225 is 46 000 when rounded off to the nearest thousand.
Examples:
53 609 is 54 000 when rounded off to the nearest thousand.
36 529 is 37 000 when rounded off to the nearest thousand.
Steps to round numbers to the nearest thousand
- Underline the number that we are rounding to
- Look at the digit to the right of the underlined digit
- If that number is 0-4, the underlined number stays the same all others are zeros,
- If that number is 5-9, the underlined digit goes up by 1. All others are zero.
Example:
Round to the thousands.
1,674
Rounding nearest thousand and to the nearest ten thousand place
Step 1: Identify the significant digit.
Step 2: Look behind to see if go up or remain unchanged.
Absolute Value
Math Worksheets
The absolute value of a number describes the distance of the number on the number line from 0. It does not consider which direction from 0 the number lies. The absolute value of a number is always positive.
The absolute value of 3 is 3 which means that its distance from 0 is 3 units
The absolute value of −3 is also 3 which means that its distance from 0 is 3 units
The symbol for absolute value is two straight lines || (called bars) surrounding the number or expression for which you wish to indicate absolute value.
| For example: | | 6 | = 6 which means the absolute value of 6 is 6. | − 6 | = 6 which means the absolute value of -6 is 6. |
| | 3 − 7 | = | −4 | = 4 | |
| | 6 + 3(−5) | = | 6 − 15 | = | −9 | = 9 |
Number Sequences
Number sequences are ordered lists of numbers that follow a particular pattern or rule. These sequences can be either finite or infinite, and can have different types of patterns. Some number sequences have a simple pattern, such as adding a fixed number to each term, while others may have more complex patterns that are not immediately obvious.
In these lessons, we will look at various types of number sequences and how to solve problems related to number sequences. In another set of lessons, we have some examples of Integer Word Problems that involve two unknowns.
Arithmetic and geometric sequences are two common types of number sequences that follow specific patterns.
An arithmetic sequence is a sequence in which each term is obtained by adding a fixed number to the previous term. For example, 2, 4, 6, 8, 10, 12, … is an arithmetic sequence, where each term is obtained by adding 2 to the previous term. The fixed number that is added to each term is called the common difference.
A geometric sequence, on the other hand, is a sequence in which each term is obtained by multiplying the previous term by a fixed number. For example, 2, 4, 8, 16, 32, 64, … is a geometric sequence, where each term is obtained by multiplying the previous term by 2. The fixed number that is multiplied by each term is called the common ratio.
The following diagrams give the formulas for Arithmetic Sequence and Geometric Sequence. Scroll down the page for examples and solutions.

How To Find The Next Term In A Number Sequence?
A number sequence is a list of numbers arranged in a row. Let us look at two examples below.
(i) 4, 6, 1, 10, 14, 5, …
(ii) 4, 7, 10, 13, ….
Number sequence (i) is a list of numbers without order or pattern. You cannot tell what number comes after 5.
Number sequence (ii) has a pattern. Do you observe that each number is obtained by adding 3 to the preceding number (i.e. the number just before it)?
In these lesson, we will only study number sequences with patterns.
Some other examples of number sequences are:
| Number Sequence | Pattern |
| 3, 6, 9, 12, … | add 3 |
| 12, 17, 22, 27, … | add 5 |
| 70, 65, 60, 55, … | subtract 5 |
| 15, 19, 23, 27, … | add 4 |
| 81, 27, 9, 3, … | divide by 3 |
How To Complete Missing Terms In A Number Sequence?
Each of the number in the sequence is called a term. In order to find the missing terms in a number sequence, we must first find the pattern of the number sequence.
Example:
Find the missing terms in the following sequence:
8, ______, 16, ______, 24, 28, 32
Solution:
To find the pattern, look closely at 24, 28 and 32. Each term in the number sequence is formed by adding 4 to the preceding number. So, the missing terms are 8 + 4 = 12 and 16 + 4 = 20. Check that the pattern is correct for the whole sequence from 8 to 32.
Example:
What is the value of n in the following number sequence?
16, 21, n, 31, 36
Solution:
We find that the number pattern of the sequence is “add 5” to the preceding number.
So, n = 21 + 5 = 26
How To Find The Next Term In A Number Sequence?
The following video shows some examples of how to determine the next term in a number sequence.
Examples:
Find the next number
- 1, 8, 15, 22, …
- 1, 8, 64, 512, …
- 1, 8, 27, 64, …
- 1, 8, 16, 15, …
How To Find The nth Term Of An Arithmetic Sequence
Example:
7, 9, 11, 13, 15, …
How To Find The nth Term Of A Geometric Sequence
Example:
5, 10, 20, 40, …
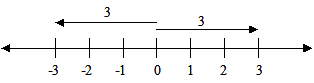
Leave a Reply