If P and Q are two non-empty sets, then a function f from P to Q is a subset of P x Q, with two important restrictions
- ∀ a ∈ P, (a, b) ∈ f for some b ∈ Q
- If (a, b) ∈ f and (a, c) ∈ f then b = c.
Note1: There may be some elements of the Q which are not related to any element of set P.
2. Every element of P must be related with at least one element of Q.
Example1: If a set A has n elements, how many functions are there from A to A?
Solution: If a set A has n elements, then there are nn functions from A to A.
Representation of a Function
The two sets P and Q are represented by two circles. The function f: P → Q is represented by a collection of arrows joining the points which represent the elements of P and corresponds elements of Q
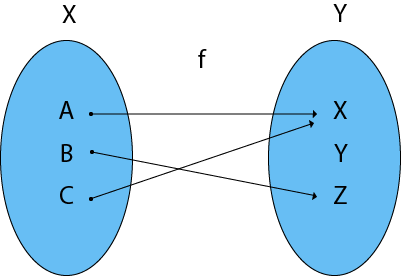
Example1:
- Let X = {a, b, c} and Y = {x, y, z} and f: X → Y such that
- f= {(a, x), (b, z), (c, x)}
Then f can be represented diagrammatically as follows
Example2: Let X = {x, y, z, k} and Y = {1, 2, 3, 4}. Determine which of the following functions. Give reasons if it is not. Find range if it is a function.
- f = {(x, 1), (y, 2), (z, 3), (k, 4)
- g = {(x, 1), (y, 1), (k, 4)
- h = {(x, 1), (x, 2), (x, 3), (x, 4)
- l = {(x, 1), (y, 1), (z, 1), (k, 1)}
- d = {(x, 1), (y, 2), (y, 3), (z, 4), (z, 4)}.
Solution:
- It is a function. Range (f) = {1, 2, 3, 4}
- It is not a function because every element of X does not relate with some element of Y i.e., Z is not related with any element of Y.
- h is not a function because h (x) = {1, 2, 3, 4} i.e., element x has more than one image in set Y.
- d is not a function because d (y) = {2, 3} i.e., element y has more than image in set Y.
Leave a Reply