Generating function is a method to solve the recurrence relations.
Let us consider, the sequence a0, a1, a2….ar of real numbers. For some interval of real numbers containing zero values at t is given, the function G(t) is defined by the series
G(t)= a0, a1t+a2 t2+⋯+ar tr+…………equation (i)
This function G(t) is called the generating function of the sequence ar.
Now, for the constant sequence 1, 1, 1, 1…..the generating function is
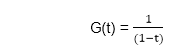
It can be expressed as
G(t) =(1-t)-1=1+t+t2 +t3+t4+⋯[By binomial expansion]
Comparing, this with equation (i), we get
a0=1,a1=1,a2=1 and so on.
For, the constant sequence 1,2,3,4,5,..the generating function is
G(t) = 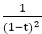 because it can be expressed as
because it can be expressed as
G(t) =(1-t)-2=1+2t+3t2 +4t3+⋯+(r+1) tr
Comparing, this with equation (i), we get
a0=1,a1=2,a2=3,a3=4 and so on.
The generating function of Zr,(Z≠0 and Z is a constant)is given by
G(t)= 1+Zt+Z2 t2+Z3 t3+⋯+Zr tr
G(t)=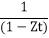 [Assume |Zt|<1]
[Assume |Zt|<1]
So, G(t)=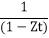 generates Zr,Z≠0
generates Zr,Z≠0
Also,If a(1)r has the generating function G1(t) and a(2)r has the generating function G2(t), then λ1 a(1)r+λ2 a(2)r has the generating function λ1 G1(t)+ λ2 G2(t). Here λ1 and λ2 are constants.
Application Areas:
Generating functions can be used for the following purposes –
- For solving recurrence relations
- For proving some of the combinatorial identities
- For finding asymptotic formulae for terms of sequences
Example: Solve the recurrence relation ar+2-3ar+1+2ar=0
By the method of generating functions with the initial conditions a0=2 and a1=3.
Solution: Let us assume that
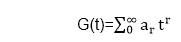
Multiply equation (i) by tr and summing from r = 0 to ∞, we have
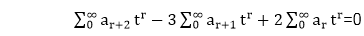
(a2+a3 t+a4 t2+⋯)-3(a1+a2 t+a3 t2+⋯)+2(a0+a1 t+a2 t2+⋯)=0
[∴ G(t)=a0+a1 t+a2 t2+⋯]
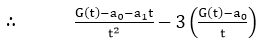 +2G(t)=0…………equation (ii)
+2G(t)=0…………equation (ii)
Now, put a0=2 and a1=3 in equation (ii) and solving, we get
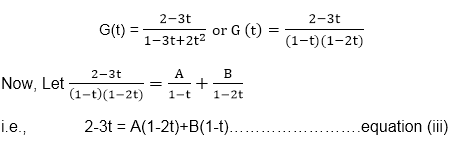
Put t=1 on both sides of equation (iii) to find A. Hence
-1=- A ∴ A = 1
Put t=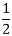 on both sides of equation (iii) to find B. Hence
on both sides of equation (iii) to find B. Hence
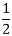 =
=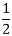 B ∴ B = 1
B ∴ B = 1
Thus G (t) = 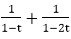 .Hence,ar=1+2r.
.Hence,ar=1+2r.
Leave a Reply