Inclusion-Exclusion Principle

Let A, B be any two finite sets. Then n (A ∪ B) = n (A) + n (B) – n (A ∩ B)

Here “include” n (A) and n (B) and we “exclude” n (A ∩ B)

Example 1:

Suppose A, B, C are finite sets. Then A ∪ B ∪ C is finite and n (A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(A ∩ C) – n(B ∩ C) + n(A ∩ B ∩ C)

Example 2:

In a town of 10000 families it was found that 40% of families buy newspaper A, 20% family buy newspaper B, 10% family buy newspaper C, 5% family buy newspaper A and B, 3% family buy newspaper B and C and 4% family buy newspaper A and C. If 2% family buy all the newspaper. Find the number of families which buy

1. Number of families which buy all three newspapers.
2. Number of families which buy newspaper A only
3. Number of families which buy newspaper B only
4. Number of families which buy newspaper C only
5. Number of families which buy None of A, B, C
6. Number of families which buy exactly only one newspaper
7. Number of families which buy newspaper A and B only
8. Number of families which buy newspaper B and C only
9. Number of families which buy newspaper C and A only
10. Number of families which buy at least two newspapers
11. Number of families which buy at most two newspapers
12. Number of families which buy exactly two newspapers

Solution:

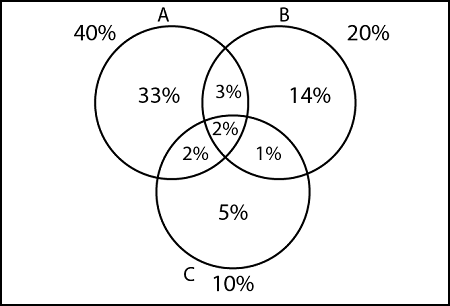
1. Number of families which buy all three newspapers:

1. n (A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(A ∩ C) – n(B ∩ C) + n(A ∩ B ∩ C)  
2. n (A ∪ B ∪ C) = 40 + 20 + 10 – 5 – 3 – 4 + 2 = 60%  

2. Number of families which buy newspaper A only

1. = 40 – 7 = 33%  

3. Number of families which buy newspaper B only

1. = 20 – 6 = 14%  

4. Number of families which buy newspaper C only

1. = 10 – 5 = 5%  

5. Number of families which buy None of A, B, and C

n (A ∪B ∪C)c = 100 - n (A ∪ B ∪ C)
n (A ∪B ∪C)c = 100 - [40 + 20 + 10 - 5- 3- 4 + 2]
n (A ∪B ∪C)c = 100 - 60 = 40 %

6. Number of families which buy exactly only one newspaper

1. = 33 + 14 + 5 = 52%  

7. Number of families which buy newspaper A and B only

1. = 3%  

8. Number of families which buy newspaper B and C only

1. = 1%  

9. Number of families which buy newspaper C and A only

1. = 2%  

10. Number of families which buy at least two newspapers

1. = 8%  

11. Number of families which buy at most two newspapers

1. = 98%  

12. Number of families which buy exactly two newspapers

1. = 6%