Theorem: If A and B are two independent events, then the probability that both will occur is equal to the product of their individual probabilities.
P(A∩B)=P(A)xP(B)
Proof: Let event
A can happen is n1ways of which p are successful
B can happen is n2ways of which q are successful
Now, combine the successful event of A with successful event of B.
Thus, the total number of successful cases = p x q
We have, total number of cases = n1 x n2.
Therefore, from definition of probability
P (A and B) =P(A∩B)=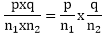
We have P(A) =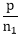 ,P(B)=
,P(B)=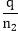
So, P(A∩B)=P(A)xP(B)
If, there are three independent events A, B and C, then
P(A∩B∩C)=P((A∩B)∩C)= P(A∩B)xP(C)
=P(A) x P(B) x P(C).
In general, if there are n independent events, then
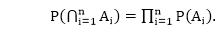
Example: A bag contains 5 green and 7 red balls. Two balls are drawn. Find the probability that one is green and the other is red.
Solution: P(A) =P(a green ball) =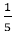
P(B) =P(a red ball) =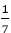
By Multiplication Theorem
P(A) and P(B) = P(A) x P(B) =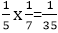
Leave a Reply