(a) Homogeneous Linear Difference Equations and Particular Solution:
We can find the particular solution of the difference equation when the equation is of homogeneous linear type by putting the values of the initial conditions in the homogeneous solutions.
Example1: Solve the difference equation 2ar-5ar-1+2ar-2=0 and find particular solutions such that a0=0 and a1=1.
Solution: The characteristics equation is 2s2-5s+2=0
(2s-1)(s-2)=0
s = 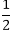 and 2.
and 2.
Therefore, the homogeneous solution of the equation is given by
ar(h)= C1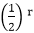 +C2 .2r……….equation (i)
+C2 .2r……….equation (i)
Putting r=0 and r=1 in equation (i), we get
a0=C1+C2=0………..equation (a)
a1=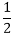 C1+2C2=1………..equation.(b)
C1+2C2=1………..equation.(b)
Solving eq (a) and (b), we have
C1=-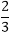 and C2=
and C2=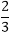
Hence, the particular solution is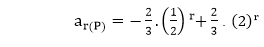
Example2: Solve the difference equation ar-4ar-1+4ar-2=0 and find particular solutions such that a0=0 and a1=6.
Solution: The characteristics equation is
s2-4s+4=0 or (s-2)2=0 s = 2, 2
Therefore, the homogeneous solution of the equation is given by
ar(n)=(C1+C2 r).2r………….. equation (i)
Putting r = 0 and r = 1 in equation (i), we get
a0=(C1+0).20 = 1 ∴C1=1
a1=(C1+C2).2=6 ∴C1+C2=3⇒C2=2
Hence, the particular solution is
ar(P)=(1+2r).2r.
Example3: Solve the difference equation 9ar-6ar-1+ar-2=0 satisfying the conditions a0=0 and a1=2.
Solution: The characteristics equation is 9s2-6s+1=0 or (3s-1)2=0
s =
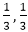
Therefore, the homogeneous solution of the equation is given by
ar(h)=(C1+C2 r).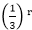 ……….equation (i)
……….equation (i)
Putting r = 0 and r = 1 in equation (i), we get
a0=C_1=0
a1= (C1+C2).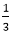 =2. ∴C1+C2=6⇒C2=6
=2. ∴C1+C2=6⇒C2=6
Hence, the particular solution is
ar(P)=6r.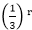 .
.
(b) Non-Homogeneous Linear Difference Equations and Particular Solution:
There are two methods to find the particular solution of a non-homogeneous linear difference equation. These are as follows:
- Undetermined coefficients method
- E and ∆ operator method.
1. Undetermined Coefficients Method: This method is used to find a particular solution of non-homogeneous linear difference equations, whose R.H.S term R (n) consist of terms of special forms.
In this method, firstly we assume the general form of the particular solutions according to the type of R (n) containing some unknown constant coefficients, which have to be determined. Then according to the difference equation, we will determine the exact solution.
The general form of a particular solution to be assumed for the special forms of R (n), to find the exact solution is shown in the table.
| Form of R (n) | General form to be assumed |
|---|---|
| Z, here z is constant | A |
| Zr, here z is constant | Zr |
| P (r), a polynomial of degree n | A0 rn+A1 rn-1+⋯..An |
| Zr. P (r), here P(r) is a polynomial of the nth degree in r. Z is a constant. | [A0 rn+A1 rn-1+⋯..An].Zr |
Example1: Find the particular solution of the difference equation ar+2-3ar+1+2ar=Zr ……..equation (i)
Where Z is some constant.
Solution: The general form of solution is = A. Zr
Now putting this solution on L.H.S of equation (i), we get
= A Zr+2-3AZr+1+2AZr=(Z2-3Z+2) A Zr………equation (ii)
Equating equation (ii) with R.H.S of equation (i), we get
(Z2-3Z+2)A=1
A =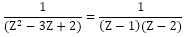 (Z≠1, Z≠2)
(Z≠1, Z≠2)
Therefore, the particular solution is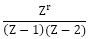
Example2: Find the particular solution of the difference equation ar+2-5ar+1+6ar=5r ………….equation (i)
Solution: Let us assume the general form of the solution= A. 5r.
Now to find the value of A, put this solution on L.H.S of the equation (i), then this becomes
= A. 5r+2-5.A5r+1+6.A5r
= 25A. 5r-25A.5r+6A.5r
= 6A.5r …………equation (ii)
Equating equation (ii) to R.H.S of equation (i), we get
A =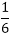
Therefore, the particular solution of the difference equation is =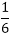 .5r.
.5r.
Example3: Find the particular solution of the difference equation ar+ 2+ar+1+ar=r.2r……….equation (i)
Solution: Let us assume the general form of the solution = (A0+A1r). 2^r
Now, put these solutions in the L.H.S of the equation (i), we get
= 2r+2 [A0+A1 (r+2)]+2r+1 [A0+A1 (r+1)]+2r (A0+A1 r)
= 4. 2r (A0+A1 r+2A1 )+2.2r (A0+A1 r+A1 )+2r (A0+A1 r)
= r. 2r (7A1 )+2r (7A0+10A1)…………equation (ii)
Equating equation (ii) with R.H.S of equation (i), we get
7A1=1 ∴ A1=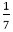
7A0+10A1=0 ∴ A0=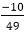
Therefore, the particular solution is 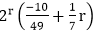
2. E and ∆ operator Method:
Definition of Operator E: The operator of E on f(x) means that give an increment to the value of x in the function. The operation of E is, put (x+h) in the function wherever there is x. Here h is increment quantity. So Ef(x) = f(x+h)
Here, E is operated on f(x), therefore, E is a symbol known as shift operator.
Definition of Operator∆: The operation ∆ is an operation of two steps.
Firstly, x in the function is incremented by a constant and then former is subtracted from the later i.e.,
∆f(x)=f(x+h)-f(x)
Theorem1: Prove that E ≅1+∆.
Proof: The operation of ∆ on f(x) is of two steps. First, increment the value of x in the function. So, whenever, there is x in f(x) put x+h (here h is constant increment), which means operation of E on f(x) i.e.,
f (x+h)=Ef(x).
Second, subtract the original function from the value obtained in the first step, hence
∆f(x)=Ef(x)-1f(x)=(E-1)f(x)
So, the operation of ∆ on f(x) is equivalent to the operation of (E-1) on f(x).
Therefore, we have
E ≅1+∆.
Theorem2: Show that En f(x)=f(x+nh).
Proof: We know that E f(x) =f (x+h)
Now En f(x)=E.E.E.E………n times f(x)
= En-1 [E f(x)] = En-1 f(x+h)
= En-2 [E f(x+h)] = En-2 f(x+2h)
………………….
………………….
= E f[x+ (n-1) h] = f(x+nh).
Theorem3: Show that E Cf(x) = CE f(x)
Proof: We know that E C f(x) = C f(x+h) = CE f(x+h). Hence Proved.
There is no effect of the operation of E on any constant. Therefore, the operation of E on any constant will be equal to constant itself.
By E and ∆ operator method, we will find the solution of
C0 yn+r+C1 yn+r-1+C2 yn+r-2+⋯+Cn yn=R (n)…………..equation (i)
Equation (i) can be written as
C0 Er yn+C1 Er-1 yn+C2 Er-2 yn+⋯+Cn yn=R (n)
(C0 Er+C1 Er-1+C2 Er-2+⋯+Cn) yn=R (n)
Putting C0 Er+C1 Er-1+C2 Er-2+⋯+Cn=P(E)
So P (E) yn=R (n)
∴ yn=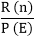 …………….equation (ii)
…………….equation (ii)
To find the particular solution of (ii) for different forms of R (n), we have the following cases.
Case1: When R (n) is some constant A.
We know that, the operation of E on any constant will be equal to the constant itself i.e.,
EA=A
Therefore, P (E) A = (C0 Er+C1 Er-1+C2 Er-2+⋯+Cn)A
= (C0+C1+C2+⋯+Cn)A
= P (1) A
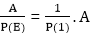
Therefore, using equation (ii), the particular solution of (i) is
yn=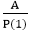 ,P(1)≠0
,P(1)≠0
P (1) is obtained by putting E = 1 in P (E).
Case2: When R (n) is of the form A. Zn, where A and Z are constants
We have, P (E) (A. Zn)={C0 Er+C1 Er-1+⋯+ Cn} (A.Zn)
=A{C0 Zr+n+C1 Zr+n-1+⋯+Cn Zn}
= A{C0 Zr+C1 Zr-1+⋯+Cn }. Zn
=AP(Z).Zn
To get, P (Z) put E=Z in P (E)
Therefore, 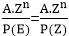 , provided P (Z) ≠ 0
, provided P (Z) ≠ 0
Thus, yn=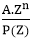 , P (Z) ≠ 0
, P (Z) ≠ 0
If A = 1, then yn=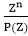
When P (Z) = 0 then for equation
(i) (E-Z) yn= A. Zn
For this, the particular solution becomes A. 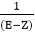 Zn=A. n Zn-1
Zn=A. n Zn-1
(ii) (E-Z)2 yn= A. Zn
For this, the particular solution becomes 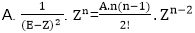
(iii) (E-Z)3 yn= A. Zn
For this, the particular solution becomes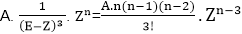 and so on.
and so on.
Case3: When R (n) be a polynomial of degree m is n.
We know that E≅1+∆
So, P (E) =P (1+∆)
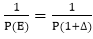
Which can be expanded in ascending power of ∆ as far as upto ∆m
⇒ 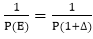 =(b0+b1 ∆+b2 ∆+⋯.+bm ∆m+⋯)
=(b0+b1 ∆+b2 ∆+⋯.+bm ∆m+⋯)
⇒ 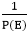 .R(n)=( b0+b1 ∆+b2 ∆+⋯.+bm ∆m+⋯).R(n)
.R(n)=( b0+b1 ∆+b2 ∆+⋯.+bm ∆m+⋯).R(n)
= b0 R(n)+b1 ∆ R(n)+⋯+bm ∆m R(n)
All other higher terms will be zero because R (n) is a polynomial of degree m.
Thus, the particular solution of equation (i), in this case will be
yn=b0 R(n)+b1 ∆ R(n)+⋯.+bm ∆m R(n).
Case4: When R (n) is of the form R(n).Zn,where R(n) is a polynomial of degree m and Z is some constant
We have Er[Zn R(n)]=Zr+n R (n+r)=Zr.Zn.Er.R(n)=Zn (ZE)rR(n)
Similarly, we have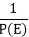 [Zn R(n)]=Zn
[Zn R(n)]=Zn 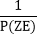 .(R(n))= Zn [P(Z+Z∆)]-1.R(n)
.(R(n))= Zn [P(Z+Z∆)]-1.R(n)
Thus, the particular solution of equation (i), in this case will be
yn=Zn [P(Z+Z∆)]-1.R(n)
Example1: Find the particular solution of the difference equation
2ar+1-ar=12.
Solution: The above equation can be written as
(2E-1) ar=12
The particular solution is given by
ar=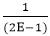 .12
.12
Put E=1, in the equation. The particular solution is ar=12
Example2: Find the particular solution of the difference equation ar-4ar-1+4ar-2=2r.
Solution: The above equation can be written as
(E2-4E+4) ar=2r
Therefore, P (E) = E2-4E+4 = (E-2)2
Thus, the particular solution is given by
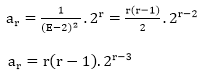
Leave a Reply