Spanning Tree

A subgraph T of a connected graph G is called spanning tree of G if T is a tree and T include all vertices of G.

Minimum Spanning Tree:

Suppose G is a connected weight graph i.e., each edge of G is assigned a non-negative number called the weight of edge, then any spanning tree T of G is assigned a total weight obtained by adding the weight of the edge in T.

A minimum spanning tree of G is a tree whose total weight is as small as possible.

Kruskal’s Algorithm to find a minimum spanning tree: This algorithm finds the minimum spanning tree T of the given connected weighted graph G.

1. Input the given connected weighted graph G with n vertices whose minimum spanning tree T, we want to find.
2. Order all the edges of the graph G according to increasing weights.
3. Initialize T with all vertices but do include an edge.
4. Add each of the graphs G in T which does not form a cycle until n-1 edges are added.

Example1: Determine the minimum spanning tree of the weighted graph shown in fig:

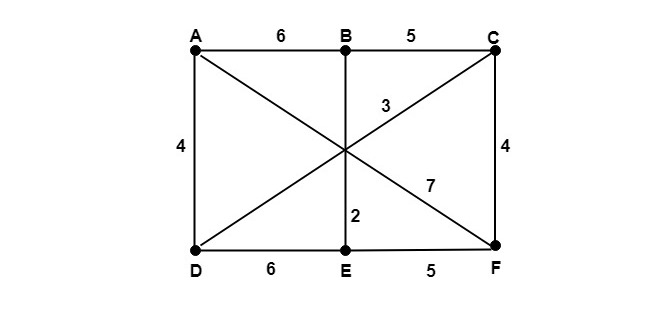
Solution: Using kruskal’s algorithm arrange all the edges of the weighted graph in increasing order and initialize spanning tree T with all the six vertices of G. Now start adding the edges of G in T which do not form a cycle and having minimum weights until five edges are not added as there are six vertices.

Edges       Weights       Added or Not
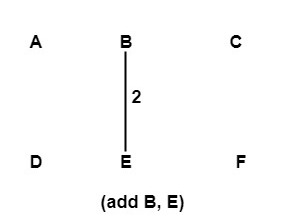
(B, E)           2                   Added
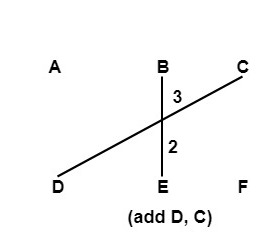
(C, D)           3                   Added
(A, D)           4                   Added
(C, F)           4                   Added
(B, C)           5                   Added
(E, F)           5                   Not added
(A, B)           6                   Not added
(D, E)           6                   Not added
(A, F)           7                   Not added

Step1:

Step2:

Step3:

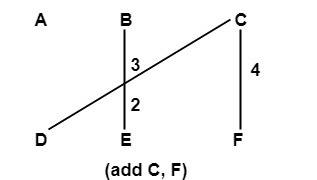
Step4:

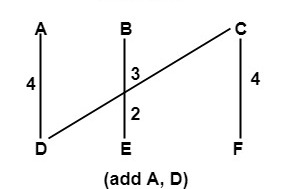
Step5:

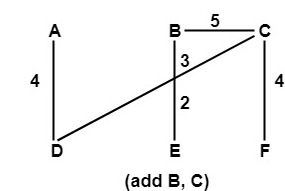
Step6: Edge (A, B), (D, E) and (E, F) are discarded because they will form the cycle in a graph.

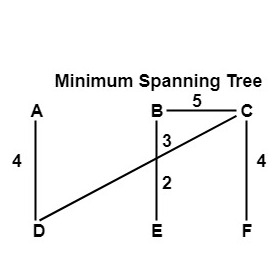
So, the minimum spanning tree form in step 5 is output, and the total cost is 18.

Example2: Find all the spanning tree of graph G and find which is the minimal spanning tree of G shown in fig:

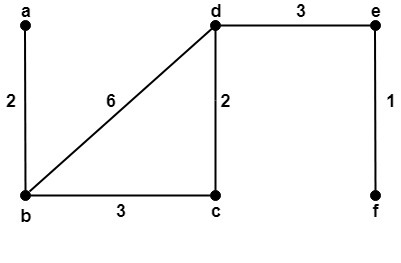
Solution: There are total three spanning trees of the graph G which are shown in fig:

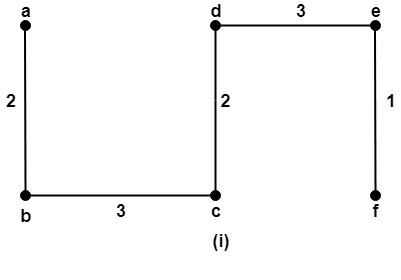
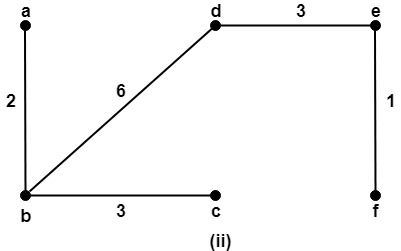
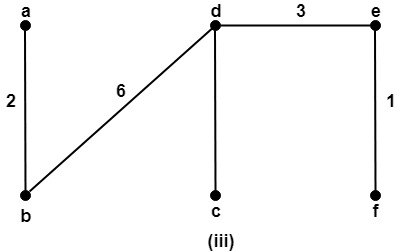
To find the minimum spanning tree, use the KRUSKAL’S ALGORITHM. The minimal spanning tree is shown in fig:

Edges       Weights       Added or Not
(E, F)           1                   Added
(A, B)           2                   Added
(C, D)           2                   Added
(B, C)           3                   Added
(D, E)           3                   Added
(B, D)           6                   Not Added