The different types of triangles may be classified by their side lengths, by their internal angles or by a combination of both their side lengths and their internal angles. Basically, there are six types of triangles that can be classified either by their sides or by their angles.
- Scalene triangle
- Isosceles triangle
- Equilateral triangle
- Right triangle
- Obtuse triangle
- Acute triangle
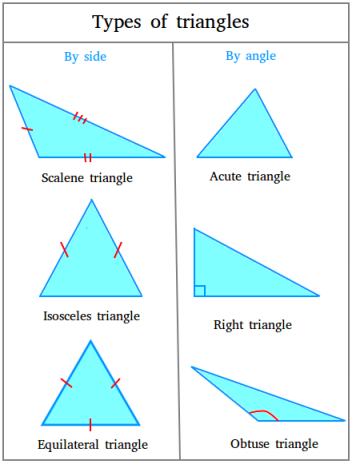
Types of triangles classified by their sides only.
A triangle classified by its sides only can either be scalene, isosceles, or equilateral.
Scalene triangle
A scalene triangle is a triangle that has no equal sides. The following is a scalene triangle.
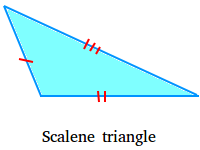
Notice the use of red marks (1, 2 and 3 marks) to show that the lengths of the sides are not the same.
Isosceles triangle
An isosceles triangle is a triangle that has two equal sides. The following is an isosceles triangle.
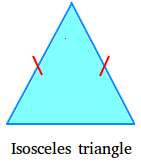
Notice the use of 1 red mark on each of the two sides that are equal.
Equilateral triangle
An equilateral triangle is a triangle that has three equal sides. The following is an equilateral triangle.
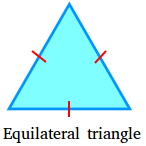
Notice the use of 1 red mark on each of the three sides that are equal.
Types of triangles classified by their angles only.
A triangle classified by its angles only can either be acute, right, or obtuse.
Right triangle:
A right triangle, also called right-angled triangle, has a 90 degrees angle.The following is a right triangle.
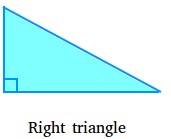
Notice that we use a small square to indicate that there is a right angle there.
Obtuse triangle:
An obtuse triangle has only one angle that is bigger than 90 degrees (Obtuse angle). The following is an obtuse triangle.
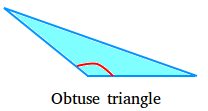
Notice that the angle that is obtuse is shown in red. The other two angles are acute angles.
Acute triangle:
In an acute triangle, also called acute-angled triangle, all angles are less than 90 degrees, so all angles are acute angles.The following is an acute triangle.
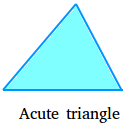
Figure summarizing the six different types of triangles based either on their sides or their angles
Classifying triangles based on their sides and their angles
We can also name triangles using angles and sides at the same time. You will end up with 7 more types.
- If a triangle has only acute angles and no equal sides, we can call that triangle acute scalene triangle.
- If a triangle has only acute angles and two equal sides, we can call that triangle acute isosceles triangle.
- If a triangle has three equal sides and only acute angles, we can call that triangle acute equilateral triangle.
- If a triangle has one right angle and no equal sides, we can call that triangle right scalene triangle.
- If a triangle has one right angle and two equal sides, we can call that triangle right isosceles triangle.
- If a triangle has two equal sides and one obtuse angle, we can call that triangle obtuse isosceles triangle.
- If a triangle has no equal sides and one obtuse angle, we can call that triangle obtuse scalene triangle.
Study also the figure below summarizing the seven types of triangles based on their sides and angles
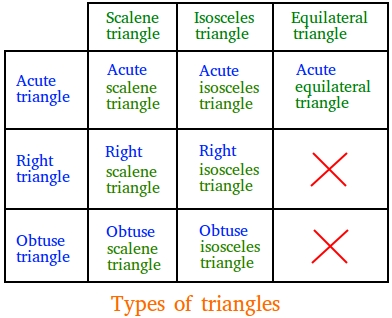
Examples on types of triangles
Example #1
The lengths of the sides of a triangle are 8 cm, 5 cm, and 6 cm. Name the triangle.
Solution
Since all the sides are of different lengths, the triangle is a scalene triangle.
Example #2
The lengths of the sides of a right triangle are 12 inches, 9 inches, and 12 inches. Name the triangle.
Solution
The triangle is a right triangle and two sides are the same. Therefore, the triangle is a right isosceles triangle.
Example #3
The lengths of the sides of a right triangle are 6 cm, 3 cm, and 5 cm and the triangle has an angle that is equal to 110 degrees. Name the triangle.
Solution
The triangle has an obtuse angle and the three sides are not the same. Therefore, the triangle is an obtuse scalene triangle.
Is it possible to have an obtuse equilateral triangle?
No it is not possible! A triangle cannot be obtuse and equilateral at the same time. An equilateral triangle cannot have an obtuse angle because all 3 angles in an equilateral triangle measure 60 degrees.
Is it possible to have a right equilateral triangle?
If the triangle is a right triangle, then one of the three angles is equal to 90 degrees. The sum of the other two angles must then add up to 90 degrees. This makes it impossible for all three angles to be equal.
Leave a Reply