In order to derive the equation of an ellipse centered at the origin, consider an ellipse that is elongated horizontally into a rectangular coordinate system and whose center is placed at the origin.
The foci are on the x-axis at (-c,0) and (c,0) and the vertices are also on the x-axis at (-a,0) and (a,0)
Let (x,y) be the coordinates of any point on the ellipse. According to the definition of an ellipse, d1 + d2 = constant.
It is very important to understand the meaning of the equation
d1 + d2 = constant in order to derive the equation of an ellipse.
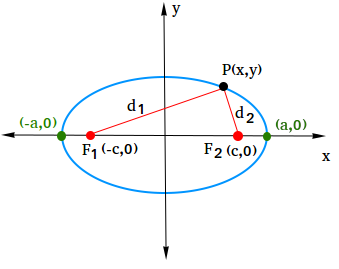
We will use the distance formula a few times in order to find different expressions for d1 and d2 and these expressions will help us derive the equation of an ellipse.
What will be a little tricky is to find what the constant is equal to. First, we will look for the constant, so gather all of your mental energy. The meaning of the definition is that no matter where you put (x,y), you will always get the same constant.
Since it does not matter where we put (x,y), we should put it on the x-axis. Why? It is because it will be easier to find what the constant is equal to. So here we go! The figure below shows the point (x,y) on the x-axis.
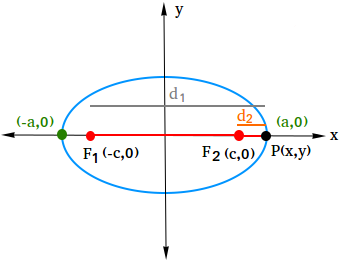
Notice that d1 is the distance between (-c, 0) and (a, 0) and d2 is the distance between (c, 0) and (a, 0)
Using the distance formula,
| d1=√(a−−c)2+(0−0)2=√(a+c)2=a+c�1=(�−−�)2+(0−0)2=(�+�)2=�+� |
| d2=√(a−c)2+(0−0)2=√(a−c)2=a−c�2=(�−�)2+(0−0)2=(�−�)2=�−� |
d1 + d2 = c + a + a – c = 2a
We have reached a milestone trying to derive the equation of an ellipse.
Now, we need to find expressions for d1 and d2. For this, we will need this figure.

Notice that when using this figure, d1 is the distance between (-c, 0) and (x, y) and d2 is the distance between (c, 0) and (x, y)
| d1=√(x−−c)2+(y−0)2d1=√(x+c)2+y2�1=(�−−�)2+(�−0)2�1=(�+�)2+�2 |
| d2=√(x−c)2+(y−0)2d2=√(x−c)2+y2�2=(�−�)2+(�−0)2�2=(�−�)2+�2 |
Let us put it all together! d1 + d2 = 2a
| √(x+c)2+y2+√(x−c)2+y2=2a(�+�)2+�2+(�−�)2+�2=2� |
Isolate a radical
√(x+c)2+y2=2a−√(x−c)2+y2(�+�)2+�2=2�−(�−�)2+�2
Square both sides
(x+c)2+y2=4a2−4a√(x−c)2+y2+(x−c)2+y2(�+�)2+�2=4�2−4�(�−�)2+�2+(�−�)2+�2
Expand (x + c)2 and (x – c)2
x2+2cx+c2+y2=4a2−4a√(x−c)2+y2+x2−2cx+c2+y2�2+2��+�2+�2=4�2−4�(�−�)2+�2+�2−2��+�2+�2
Simplify by getting rid of x2, c2, and y2 from both sides of the equation.
2cx=4a2−4a√(x−c)2+y2−2cx2��=4�2−4�(�−�)2+�2−2��
Isolate the radical
4cx−4a2=−4a√(x−c)2+y24��−4�2=−4�(�−�)2+�2
Divide both sides by 4
cx−a2=−a√(x−c)2+y2��−�2=−�(�−�)2+�2
Square both sides
(cx−a2)2=a2[(x−c)2+y2](��−�2)2=�2[(�−�)2+�2]
Expand (cx – a2)2 and (x – c)2
c2x2 – 2a2cx + a4 = a2(x2 – 2cx + c2 + y2)
c2x2 – 2a2cx + a4 = a2x2 -2a2cx + a2c2 + a2y2
Simplify by getting rid of – 2a2cx
c2x2 + a4 = a2x2 + a2c2 + a2y2
Rearrange the terms so that terms that have the variable x or the variable y are on the same side of the equation and everything else is on the other side of the equation.
c2x2 – a2x2 – a2y2 = a2c2 – a4
Factor out x2 and a2
x2(c2 – a2) – a2y2 = a2(c2 – a2)
Multiply both sides by -1
x2(a2 – c2 ) + a2y2 = a2(a2 – c2)
We just need 1 little piece of information to finish this problem off and derive the equation of an ellipse! Take a look at the following figure. We now place (x,y) on the y-axis. We also define co-vertices located on the y-axis at (0,b) and (0, -b).
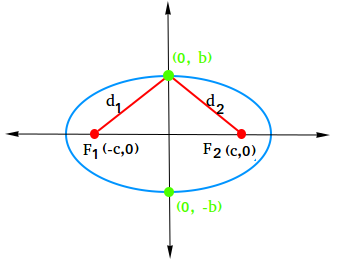
| d1=√(b−0)2+(0−−c)2=√b2+c2�1=(�−0)2+(0−−�)2=�2+�2 |
| d2=√(b−0)2+(0−c)2=√b2+c2�2=(�−0)2+(0−�)2=�2+�2 |
d1 + d2 = 2a
| √b2+c2+√b2+c2=2a�2+�2+�2+�2=2� |
| 2√b2+c2=2a2�2+�2=2� |
Divide both sides by 2
| √b2+c2=a�2+�2=� |
Square both sides
b2 + c2 = a2
Isolate b2
b2 = a2 – c2
Substitute b2 for a2 – c2 in x2(a2 – c2 ) + a2y2 = a2(a2 – c2)
x2b2 + a2y2 = a2b2
Divide both sides by a2b2
| x2b2a2b2+a2y2a2b2=a2b2a2b2�2�2�2�2+�2�2�2�2=�2�2�2�2 |
| x2a2+y2b2=1�2�2+�2�2=1 |
This is how to derive the equation of an ellipse when the horizontal major axis is centered at the origin.
Leave a Reply