Pythagorean theorem

The Pythagorean Theorem was named after famous Greek mathematician Pythagoras. It is an important formula that states the following: a² + b² = c²

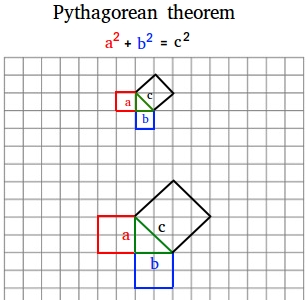
Looking at the figure above, did you make the following important observation? This may help us to see why the formula works.

• The red square has 2 triangles in it 
• The blue square has also 2 triangles in it
• The black square has 4 of the same triangle in it

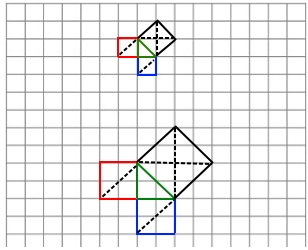
Therefore, area of red square  + area of blue square = area of black square

Let a = the length of a side of the red square

Let b = the length of a side of the blue square

Let c = the length of a side of the black square

Therefore, a² + b² = c²Generally speaking, in any right triangle, let c be the length of the longest side (called hypotenuse) and let a and b be the length of the other two sides (called legs).

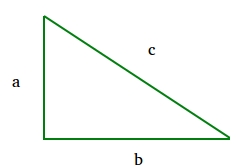
The theorem states that the length of the hypotenuse squared is equal to the length of side a squared plus the length of side b squared. Written as an equation, c² = a² + b²

Thus, given two sides, the third side can be found using the formula.

We will illustrate with examples, but before proceeding, you should know how to find the square root of a number and how to solve equations using subtraction.

Examples showing how to use the Pythagorean theorem

Exercise #1

Let a = 3 and b = 4. Find c, or the longest side

c² = a² + b²

c² = 3² + 4²

c²= 9 + 16

c² = 25

c = √25

The sign (√) means square root

c = 5

Exercise #2

Let c = 10 and a = 8. Find b, or the other leg.

c² = a² + b²

10² = 8² + b²

100 = 64 + b²

100 – 64 = 64 – 64 + b² (minus 64 from both sides to isolate b² )

36 = 0 + b²

36 = b²

b = √36 = 6

Exercise #3

Let c = 13 and b = 5. Find a

c² = a ²+ b²

13² = a² + 5²

169 = a² + 25

169 – 25 = a² + 25-25

144 = a² + 0

144 = a²

a = √144 = 12