Here, we provide you with volume formulas for some common three-dimensional figures and also for the ellipsoid and the hollow cylinder that are not so common.
Cube:
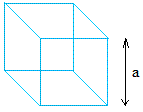
Volume = a3 = a × a × a
Cylinder:
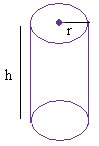
Volume = π × r2 × h
π = 3.14
h is the height
r is the radius
Rectangular solid or cuboid:
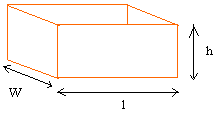
Volume = l × w × h
l is the length
w is the width
h is the height
Sphere:
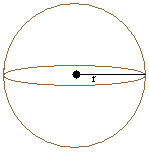
Volume = (4 × π × r3)/3
π = 3.14
r is the radius
Cone:
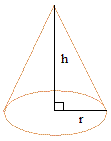
Volume = (π × r2 × h)/3
pi = 3.14
r is the radius
h is the height
Pyramid:
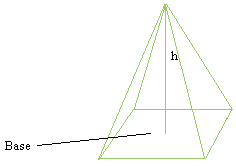
Volume = (B × h)/3
B is the area of the base
h is the height
Less common volume formulas
Ellipsoid:
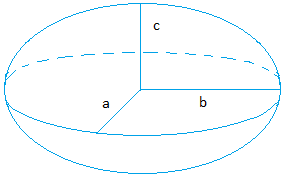
Volume = (4 × π × a × b × c)/3
Use π = 3.14
Hollow cylinder:
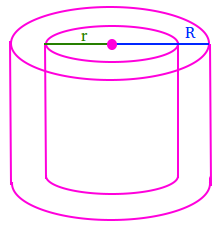
Volume = π × R2 × h – π × r2 × h
Volume = π × h ( R2 – r2)
Use π = 3.14.
How to use the volume formulas to calculate the volume
Volume of a cube
The length of a side = a = 2 cm
Volume = (2 cm) = 2 cm × 2 cm × 2 cm = 8 cm3 = 8 cubic centimeters
Volume of a cylinder
The height is 8 inches and the radius is 2 inches.
Volume = π × r2 × h = 3.14 × (2 in)2 × 8 in = 3.14 × 4 × 8 in3
Volume = 3.14 × 32 in3 = 100.48 in2 = 100.48 cubic inches
Volume of a cuboid or rectangular solid
The length is 6 cm, the width is 3 cm and the height is 5 cm.
Volume = l × w × h = 6 × 3 × 5 = 90 cm3 = 90 cubic centimeters
Volume of a sphere
The radius = r = 20
Volume = (4 × π × r3)/3 = [4 × 3.14 × (20)3]/3 = 3.14 × (20)3 × 4
Volume = 3.14 × 8000 × 4 = 3.14 × 32000 = 100480
Volume of a cone
The radius is equal to 3 and the height is equal to 4.
Volume = (π × r2 × h)/3 = [3.14 × (3)2× 4]/3 = 3.14 × 9× 4
Volume = 3.14 × 36 = 113.04
Volume of a pyramid
A pyramid has a height of 6 feet. If the base of a pyramid is a square with a length of 2 feet, find the volume.
Volume = (B × h)/3
B = area of base = 2 ft × 2 ft = 4 ft2
Volume = (4 × 6)/3 ft3 = 24/3 ft3 = 8 ft3 = 8 cubic feet
Volume of an ellipsoid
The radii of an ellipsoid are 1 cm, 2, cm, and 3 cm.
Volume = (4 × π × a × b × c)/3 = (4 × 3.14 × 1 × 2 × 3)/3
Volume = ( 3.14 × 4 × 6)/3 = ( 3.14 × 24)/3 = 81.64/3 = 25.12 cm3 = 25.12 cubic centimeters
Volume of a hollow cylinder
The outer radius is 8, the internal radius is 6, and the height is 10.
Volume = π × h ( R2 – r2) = π × 10 ( 82 – 62) = π × 10 ( 64 – 36)
Volume = π × 10(28) = π × 280 = 879.2
General formula to find the volume of prisms such as triangular prisms or rectangular prisms
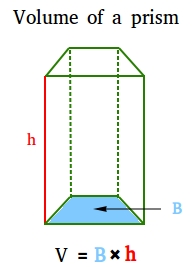
The volume of a prism is the product of the area of a base and the height of the prism.
V = Bh
A couple of examples showing how to find the volume of prisms
A triangular prism
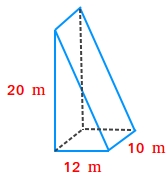
1. Find the volume of the triangular prism shown in the image above using the formula below.
V = Bh
The dimensions of the triangular base are 12 m and 20 m.
The height of the triangular prism is h = 10 m.
B = area of the triangular base = (20 times 12)/2 = 240/2 = 120 m2
V = 120 times 10 = 1200
The volume of the triangular prism is 1200 cubic meters.
A trapezoidal prism
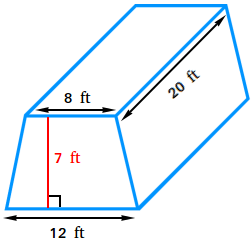
2. Find the volume of the trapezoidal prism shown in the image above using the formula below.
V = Bh
The base of the trapezoidal prism is a trapezoid with the following dimensions.
b1 = 12 ft, b2 = 8 ft, and height = 7 feet.
The height of the trapezoidal prism is the perpendicular distance or 20 ft
B = area of the base = [(b1 + b2)h]/2
B = [(12 + 8)7]/2
B = [(20)7]/2
B = 140/2
B = 70 square feet
V = 70 times 20 = 1400
The volume of the trapezoidal prism is 1400 cubic feet
Leave a Reply