Functions

It is a mapping in which every element of set A is uniquely associated at the element with set B. The set of A is called Domain of a function and set of B is called Co domain.

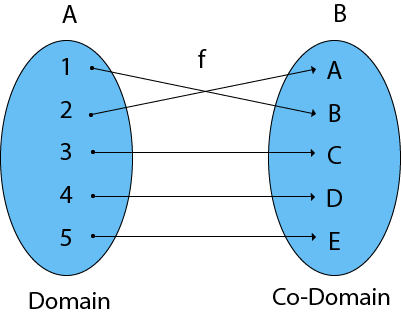
Domain, Co-Domain, and Range of a Function:

Domain of a Function: Let f be a function from P to Q. The set P is called the domain of the function f.

Co-Domain of a Function: Let f be a function from P to Q. The set Q is called Co-domain of the function f.

Range of a Function: The range of a function is the set of picture of its domain. In other words, we can say it is a subset of its co-domain. It is denoted as f (domain).

1. If f: P → Q, then f (P) = {f(x): x ∈ P} = {y: y ∈ Q | ∃ x ∈ P, such that f (x) = y}.  

Example: Find the Domain, Co-Domain, and Range of function.

1. Let x = {1, 2, 3, 4}  
2.     y = {a, b, c, d, e}  
3.     f = {(1, b), (2, a), (3, d), (4, c)  

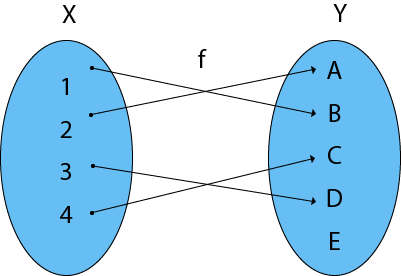
Solution:

Domain of function: {1, 2, 3, 4}
Range of function: {a, b, c, d}
Co-Domain of function: {a, b, c, d, e}