Sum Rule Principle: Assume some event E can occur in m ways and a second event F can occur in n ways, and suppose both events cannot occur simultaneously. Then E or F can occur in m + n ways.
In general, if there are n events and no two events occurs in same time then the event can occur in n1+n2……….n ways.
Example: If 8 male processor and 5 female processor teaching DMS then the student can choose professor in 8+5=13 ways.
Product Rule Principle: Suppose there is an event E which can occur in m ways and, independent of this event, there is a second event F which can occur in n ways. Then combinations of E and F can occur in mn ways.
In general, if there are n events occurring independently then all events can occur in the order indicated as n1 x n2 x n3………n ways.
Example: In class, there are 4 boys and 10 girls if a boy and a girl have to be chosen for the class monitor, the students can choose class monitor in 4 x 10 = 40 ways.
Mathematical Functions:
Factorial Function: The product of the first n natural number is called factorial n. It is denoted by n!, read “n Factorial.”
The Factorial n can also be written as
- n! = n (n-1) (n-2) (n-3)……1.
- = 1 and 0! = 1.
Example1: Find the value of 5!
Solution:
5! = 5 x (5-1) (5-2) (5-3) (5-4) = 5 x 4 x 3 x 2 x 1 = 120
Example2: Find the value of 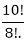
Solution: 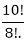 =
=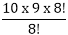 = 10 x 9=90
= 10 x 9=90
Binomial Coefficients: Binomial Coefficient is represented by nCr where r and n are positive integer with r ≤ n is defined as follows:
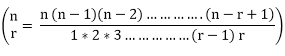
Example: 8C2 =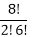 =
=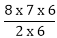 = 28.
= 28.
Leave a Reply