Graph G consists of two things:
1. A set V=V(G) whose elements are called vertices, points or nodes of G.
2. A set E = E(G) of an unordered pair of distinct vertices called edges of G.
3. We denote such a graph by G(V, E) vertices u and v are said to be adjacent if there is an edge e ={u, v}.
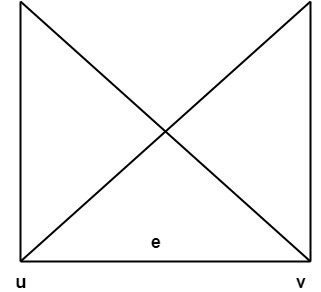
4. In such a case u and v are called the endpoint of e={u, v} and e are said to connect u and v.
Degree of a Vertex:
The degree of a vertex is the number of edges incident on a vertex v. The self-loop is counted twice. The degree of a vertex is denoted by d(v).
Example1: Consider the graph G shown in fig. Determine the degree of each vertex.
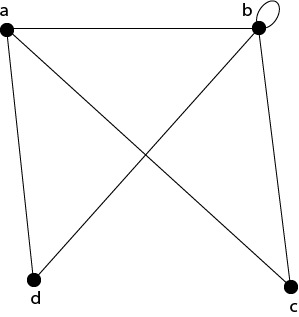
Solution: The degree of each vertex is as follows:
d(a)=3; d(b)=5; d(c) = 2; d(d)=2.
Example2: Verify that the sum of the degrees of all the vertices is even for the graph shown in fig:
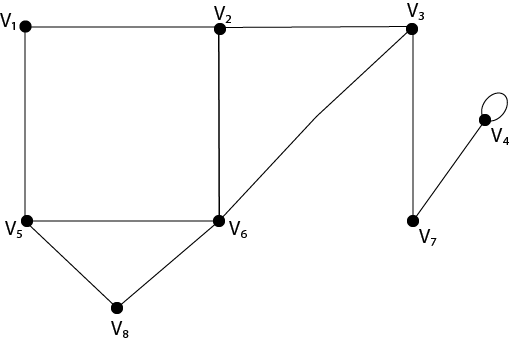
Solution: The sum of the degrees of all the vertices is:
=d (v1)+d(v2 )+d(v3 )+d(v4 )+d(v5 )+d(v6 )+d(v7 )+d(v8)
= 2+3+3+3+3+4+2+2=22, which is even.
Example3: Verify that there are even numbers of vertices of odd degrees in the graph shown in fig:
Solution: The number of vertices of degree odd is 8, and each has a degree three in the above graph. Hence, we have even number of vertices of odd degrees.
Path:
A path of length n is a sequence of n+1 vertices of a graph in which each pair of vertices is an edge of the graph.
- A Simple Path: The path is called simple one if no edge is repeated in the path, i.e., all the vertices are distinct except that first vertex equal to the last vertex.
- An Elementary Path: The path is called elementary one if no vertex is repeated in the path, i.e., all the vertices are distinct.
- Circuit or Closed Path: The circuit or closed path is a path in which starts and ends at the same vertex, i.e., v0=vn.
- Simple Circuit Path: The simple circuit is a simple path which is a circuit.
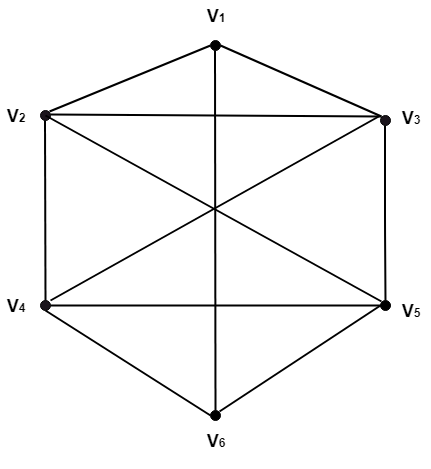
Example: Consider the graph shown in fig: Give an example of the following:
- A simple path fromV1 to V6.
- An elementary path from V1 to V6.
- A simple path which is not elementary from V1 to V6.
- A path which is not simple and starting fromV2.
- A simple circuit starting from V1
- A circuit which is not simple and starting from V2.
Solution:
- A simple path fromV1 to V6.
V1,V2,V3,V4,V5,V6. - An elementary path from V1 to V6.
V1,V2,V3,V5,V4,V6. - A simple path which is not elementary from V1 to V6.
V1,V2,V3,V5,V2,V4,V6. - A path which is not simple and starting fromV2.
V2,V3,V4,V5,V3,V4,V6. - A simple circuit starting fromV1.
V1,V2,V4,V6,V5,V3,V1 - A circuit which is not simple and starting from V2.
V2,V3,V1,V2,V5,V4,V2.
Pendant Vertex: A vertex with degree one is called a Pendant Vertex.
Pendant Edge: The only edge which is an incident with a pendant vertex is called the Pendant Edge.
Odd Vertex: A vertex having degree odd is called an odd vertex.
Even Vertex: A vertex having a degree even is called an even vertex.
Incident Edge: An edge is called incident with the vertices is connects.
Adjacent Vertices: Two vertices are called adjacent if an edge links them. If there is an edge (u, v), then we can say vertex u is adjacent to vertex v, and vertex v is adjacent to vertex u.
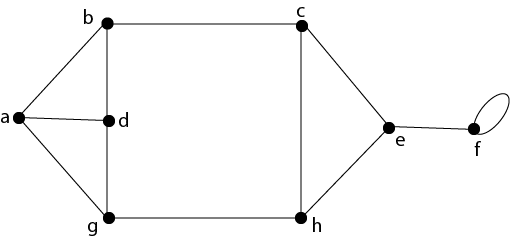
Example: Consider the graph as shown in fig:
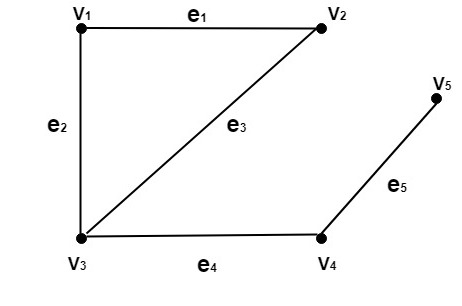
Determine the following:
- Pendant Vertices
- Pendant Edges
- Odd vertices
- Even Vertices
- Incident Edges
- Adjacent Vertices
Solution:
- The vertex V5is the pendant vertex.
- The edge (V4,V5) or e5 is the pendant edge.
- The vertices V3 and V5 are odd vertices.
- The vertices V1, V2,and V4 are even vertices.
- The edge e1 is an incident on V1, and V2.
The edge e2 is an incident on V1 and V3.
The edge e3 is an incident on V2 and V3.
The edge e4 is an incident on V3 and V4.
The edge e5 is an incident on V4 and V5. - The vertex V1 is adjacent to V2 and V3.
The vertex V2 is adjacent to V1 and V2.
The vertex V3 is adjacent to V1 and V4
The vertex V4 is adjacent to V3 and V5
The vertex V5 is adjacent to V4.
Self-Loop: A self-loop is an edge e if it has the same endpoint.
The graph shown in fig contains the self-loop at vertex b,i.e., e=(b, b).
Isolated Vertex: A vertex with degree 0 is called Isolated Vertex.
Cut Set: Consider a graph G=(V, E).A cut set for G is the smallest set of edges such that the removal of the set, disconnected the graph whereas the removal of any proper subset of this set left a connected subgraph.
Example: Consider the graph shown in fig. Determine the cut set for this group.
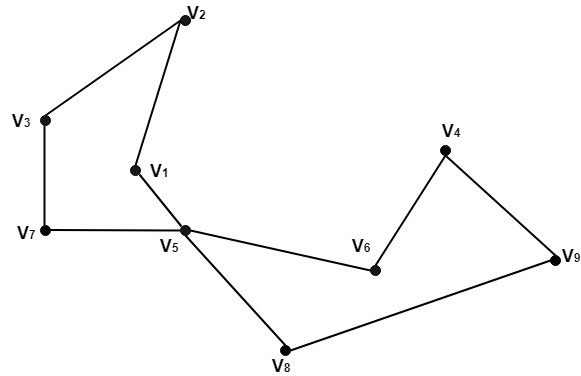
Solution: For this graph, the edge set {(V1,V5),(V7,V5)} is a cut set. After the removal of the set, we have left with a disconnected subgraph. While after the removal of any of its proper subset, we have left with a connected subgraph.
Cut Points or Cut Vertices: Consider a graph G=(V, E). A cut point for a graph G is a vertex v such that G-v has more connected components than G or disconnected.
The subgraph G-v is obtained by deleting the vertex v from graph G and also deleting the entire edges incident on v.
Example: Consider the graph shown in fig. Determine the subgraphs
(i)G-v1 (ii) G-v3 (iii) G-v5
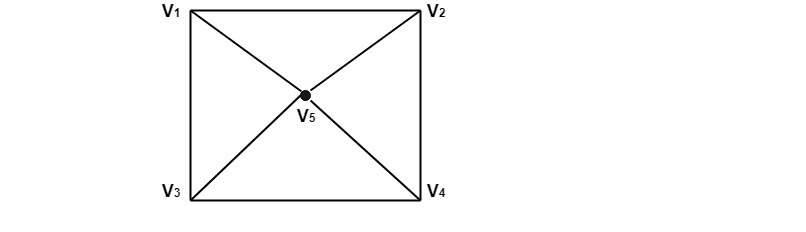
Solution:
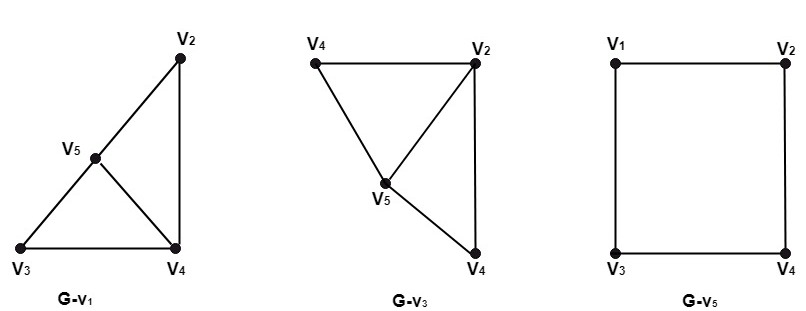
- The subgraph G-v1 is shown in fig
- The subgraph G-v3 is shown in fig
- The subgraph G-v5 is shown in fig
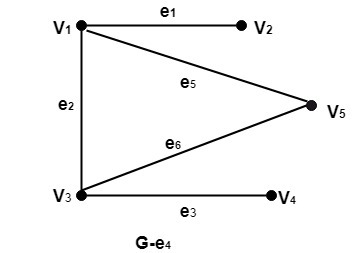
Bridge (Cut Edges): Consider a graph G=(V, E).A bridge for a graph G, is an edge e such that G-e has more connected components than G or disconnected.
Example: Consider the graph shown in fig. Determine the subgraphs
(i)G-e1 (ii) G-e3 (iii) G-e4
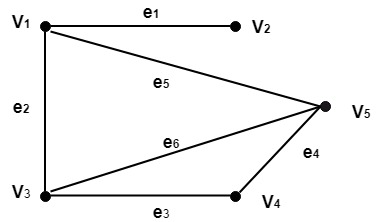
Solution:
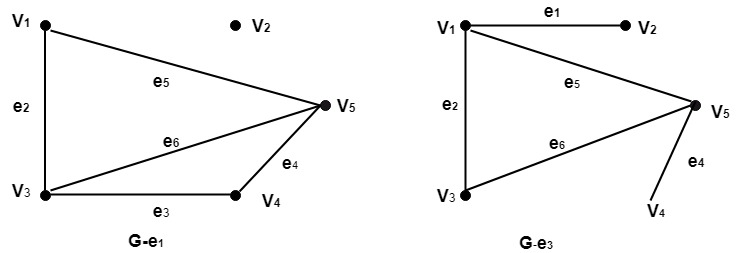
- The subgraph G-e1 is shown in fig
- The subgraph G-e3 is shown in fig
- The subgraph G-e4 is shown in fig
Leave a Reply