Suppose a salesman wants to visit a certain number of cities allotted to him. He knows the distance of the journey between every pair of cities. His problem is to select a route the starts from his home city, passes through each city exactly once and return to his home city the shortest possible distance. This problem is closely related to finding a Hamiltonian circuit of minimum length. If we represent the cities by vertices and road connecting two cities edges we get a weighted graph where, with every edge ei a number wi(weight) is associated.
A physical interpretation of the above abstract is: consider a graph G as a map of n cities where w (i, j) is the distance between cities i and j. A salesman wants to have the tour of the cities which starts and ends at the same city includes visiting each of the remaining a cities once and only once.
In the graph, if we have n vertices (cities), then there is (n-1)! Edges (routes) and the total number of Hamiltonian circuits in a complete graph of n vertices will be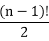 .
.
Nearest Neighbour Method:
This procedure gives reasonably good results for the travelling salesman problem. The method is as follows:
Step1: Select an arbitrary vertex and find the vertex that is nearest to this starting vertex to form an initial path of one edge.
Step2: Let v denote the latest vertex that was added to the path. Now, among the result of the vertices that are not in the path, select the closest one to v and add the path, the edge-connecting v and this vertex. Repeat this step until all the vertices of graph G are included in the path.
Step3: Join starting vertex and the last vertex added by an edge and form the circuit.
Example: Use the nearest-neighbor method to solve the following travelling salesman problem, for the graph shown in fig starting at vertex v1.
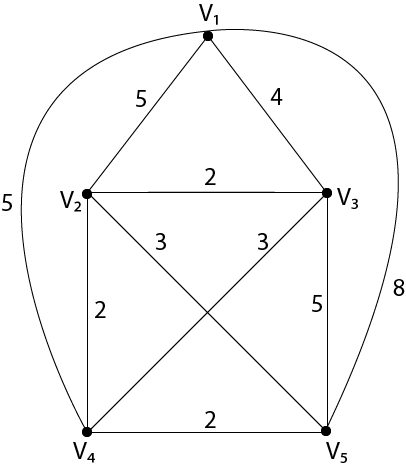
Solution: We have to start with vertex v1. By using the nearest neighbor method, vertex by vertex construction of the tour or Hamiltonian circuit is shown in fig:
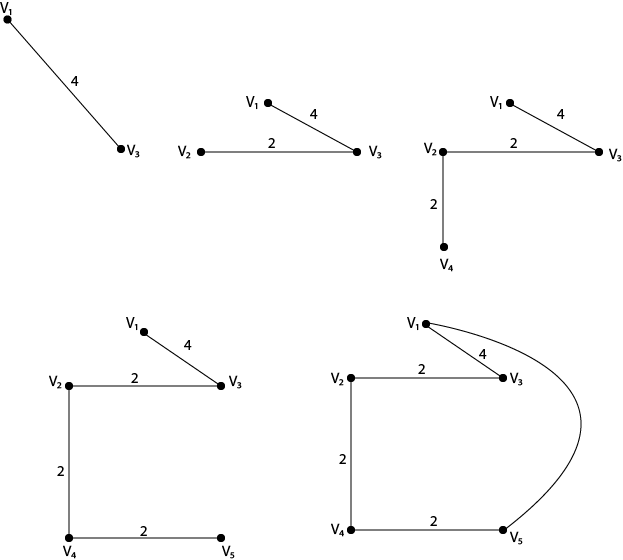
Leave a Reply