There are many properties of the binary operations which are as follows:
1. Closure Property: Consider a non-empty set A and a binary operation * on A. Then is closed under the operation *, if a * b ∈ A, where a and b are elements of A.
Example1: The operation of addition on the set of integers is a closed operation.
Example2: Consider the set A = {-1, 0, 1}. Determine whether A is closed under
- Addition
- Multiplication
Solution:
(i)The sum of elements is (-1) + (-1) = -2 and 1+1=2 does not belong to A. Hence A is not closed under addition.
(ii) The multiplication of every two elements of the set are -1 * 0 = 0; -1 * 1 =-1; -1 * -1 = 1
0 * -1 = 0; 0 * 1 = 0; 0 * 0 = 0
1 * -1 = -1; 1 * 0 = 0; 1 * 1 = 1
Since, each multiplication belongs to A hence A is closed under multiplication.
2. Associative Property: Consider a non-empty set A and a binary operation * on A. Then the operation * on A is associative, if for every a, b, c, ∈ A, we have (a * b) * c = a* (b*c).
Example: Consider the binary operation * on Q, the set of rational numbers, defined by a * b = a + b – ab ∀ a, b ∈ Q.
Determine whether * is associative.
Solution: Let us assume some elements a, b, c ∈ Q, then the definition (a*b) * c = (a + b- ab) * c = (a + b- ab) + c – (a + b- ab)c
= a + b- ab + c – ca -bc + abc = a + b + c – ab – ac -bc + abc.
Similarly, we have
a * (b * c) = a + b + c – ab – ac -bc + abc
Therefore, (a * b) * c = a * (b * c)
Hence, * is associative.
3. Commutative Property: Consider a non-empty set A,and a binary operation * on A. Then the operation * on A is associative, if for every a, b, ∈ A, we have a * b = b * a.
Example: Consider the binary operation * on Q, the set of rational numbers, defined by a * b = a2+b2 ∀ a,b∈Q.
Determine whether * is commutative.
Solution: Let us assume some elements a, b, ∈ Q, then definition a * b = a2+b2=b * a
Hence, * is commutative.
4. Identity: Consider a non-empty set A, and a binary operation * on A. Then the operation * has an identity property if there exists an element e in A such that a * e (right identity) = e * a (left identity) = a ∀ a ∈ A.
Example: Consider the binary operation * on I+, the set of positive integers defined by a * b =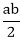
Determine the identity for the binary operation *, if exists.
Solution: Let us assume that e be a +ve integer number, then
e * a, a ∈ I+
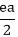 = a, e = 2……………equation (i)
= a, e = 2……………equation (i)
Similarly, a * e = a, a ∈ I+
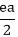 =2 or e=2………..equation (ii)
=2 or e=2………..equation (ii)
From equation (i) and (ii) for e = 2, we have e * a = a * e = a
Therefore, 2 is the identity elements for *.
5. Inverse: Consider a non-empty set A, and a binary operation * on A. Then the operation is the inverse property, if for each a ∈A,,there exists an element b in A such that a * b (right inverse) = b * a (left inverse) = e, where b is called an inverse of a.
6. Idempotent: Consider a non-empty set A, and a binary operation * on A. Then the operation * has the idempotent property, if for each a ∈A, we have a * a = a ∀ a ∈A
7. Distributivity: Consider a non-empty set A, and a binary operation * on A. Then the operation * distributes over +, if for every a, b, c ∈A, we have
a * (b + c) = (a * b) + (a * c) [left distributivity]
(b + c) * a = (b * a) + (c * a) [right distributivity]
8. Cancellation: Consider a non-empty set A, and a binary operation * on A. Then the operation * has the cancellation property, if for every a, b, c ∈A,we have
a * b = a * c ⇒ b = c [left cancellation]
b * a = c * a ⇒ b = c [Right cancellation]
Leave a Reply