The three properties of congruence are the reflexive property of congruence, the symmetric property of congruence, and the transitive property of congruence. These properties can be applied to segment, angles, triangles, or any other shape.Reflexive property of congruence
The meaning of the reflexive property of congruence is that a segment, an angle, a triangle, or any other shape is always congruent or equal to itself.
Examples
AB ≅ AB (Segment AB is congruent or equal to segment AB)
∠A ≅ ∠A (Angle A is congruent or equal to angle A)
Symmetric property of congruence
The meaning of the symmetric property of congruence is that if a figure (call it figure A) is congruent or equal to another figure (call it figure B), then figure B is also congruent or equal to figure A.
Examples
If AB ≅ CD, then CD ≅ AB
If ∠A ≅ ∠B , then ∠B ≅ ∠A
Transitive property of congruence
The meaning of the transitive property of congruence is that if a figure (call it figure A) is congruent or equal to another figure (call it figure B) and figure B is also congruent to another figure (call it C) , then figure A is also congruent or equal to figure C.
Examples
If AB ≅ CD and CD ≅ EF, then AB ≅ EF
If ∠A ≅ ∠B and ∠B ≅ ∠C, then ∠A ≅ ∠C
Naming the properties of congruence that justify the statements below.
If XY ≅ ZW, then ZW ≅ XY This is the symmetric property of congruence.
∠RTS ≅ ∠RTS This is the reflexive property of congruence.
If GF ≅ ST and ST ≅ WU, then GF ≅ WU This is the transitive property of congruence.
Applying the properties of congruence to other shapes
Reflexive property
△ABC ≅△ABC (A triangle is always congruent or equal to itself)
Symmetric property
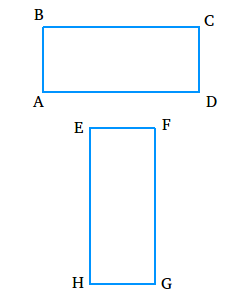
If ▭ABCD ≅ ▭EFGH, then ▭EFGH ≅ ▭ABCD
Rectangle ABCD could be the shape of your backyard and rectangle EFGH could be the shape of neighbor’s backyard.
A little exercise about the properties of congruence
Try to complete each statement using the given property
Reflexive property of congruence
∠UGD ≅ ?
Symmetric property of congruence
If SE ≅ PO, then ? ≅ ?
Transitive property of congruence
If ∠S ≅ ∠T and ∠ ? ≅ ∠U, then ∠ ? ≅ ∠ ?
Leave a Reply