The distance between a point and a line is defined to be the length of the perpendicular line segment connecting the point to the given line.
Let (x1,y1) be the point not on the line and let (x2,y2) be the point on the line.
To find the distance between the point (x1,y1) and the line with equation ax + bx + c = 0, you can use the formula below.
d=|ax1+by1+c|√a2+b2�=|��1+��1+�|�2+�2
How to calculate the distance between a point and a line using the formula
Example #1
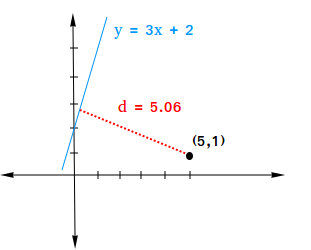
Find the distance between a point and a line using the point (5,1) and the line y = 3x + 2.
Rewrite y = 3x + 2 as ax + by + c = 0
Using y = 3x + 2, subtract y from both sides.
y – y = 3x – y + 2
0 = 3x – y + 2
3x – y + 2 = 0
a = 3, b = -1, and c = 2
x1 = 5 and y1 = 1
d=|3×5+−1×1+2|√32+(−1)2�=|3×5+−1×1+2|32+(−1)2
d=|15+−1+2|√9+1�=|15+−1+2|9+1
d=|16|√10�=|16|10
d=163.16=5.06�=163.16=5.06
Example #2
Find the distance between a point and a line using the point (-4,2) and the line y = -2x + 5.
Rewrite y = -2x + 5 as ax + by + c = 0
Using y = -2x + 5, subtract y from both sides.
y – y = -2x – y + 5
0 = -2x – y + 5
-2x – y + 5 = 0
a = -2, b = -1, and c = 5
x1 = -4 and y1 = 2
d=|−2×−4+−1×2+5|√(−2)2+(−1)2�=|−2×−4+−1×2+5|(−2)2+(−1)2
d=|8+−2+5|√4+1�=|8+−2+5|4+1
d=|11|√5�=|11|5
d=112.23=4.92�=112.23=4.92
How to calculate the distance between a point and a line using the distance formula
We can redo example #1 using the distance formula. To use the distance formula, we need two points. We already have (5,1) that is not located on the line y = 3x + 2.
We can just look for the point of intersection between y = 3x + 2 and the line that is perpendicular to y = 3x + 2 and passing through (5, 1)
The line that is perpendicular to y = 3x + 2 is given by y = (-1/3)x + b.
Use the point (5, 1) to find b by letting x = 5 and y = 1.
1 = (-1/3) × 5 + b
1 = -5/3 + b
b = 1 + 5/3 = 8/3
y = (-1/3)x + 8/3
Now, set the two equations equal to themselves
(-1/3)x + 8/3 = 3x + 2
3x + (1/3)x = 8/3 – 2
(10/3)x = (8 – 6)/3
(10/3)x = 2/3
x = (2/3) × 3/10 = 2/10 = 1/5
y = 3x + 2 = 3 × 1/5 + 2 = 3/5 + 2 = 13/5
The point of intersection between y = 3x + 2 and y = (-1/3)x + 8/3 is
(1/5, 13/5) or (0.25, 2.6)
Find the distance using the points (5,1) and (0.25, 2.6).
d=√(5−0.25)2+(1−2.6)2�=(5−0.25)2+(1−2.6)2
d=√(4.75)2+(−1.6)2�=(4.75)2+(−1.6)2
d=√22.5625+2.56�=22.5625+2.56
d=√25.1225=5.01�=25.1225=5.01
How to derive the formula to find the distance between a point and a line.
To derive the formula at the beginning of the lesson that helps us to find the distance between a point and a line, we can use the distance formula and follow a procedure similar to the one we followed in the last section when the answer for d was 5.01.
Hang in there tight. Deriving the distance between a point and a line is among of the toughest things you have ever done in life.

The steps to take to find the formula are outlined below.
1) Write the equation ax + by + c = 0 in slope-intercept form.
2) Use (x1, y1) to find the equation that is perpendicular to ax + by + c = 0
3) Set the two equations equal to each other to find expressions for the points of intersection (x2, y2)
4) Use the distance formula, (x1, y1), and the expressions found in step 3 for (x2, y2) to derive the formula.
1)
ax + by + c = 0
ax – ax + by + c = -ax
by + c = -ax
by + c – c = -ax – c
by = -ax – c
y = -ax/b – c/b
y = (-a/b)x – c/b×
2) The line that is perpendicular to y = (-a/b)x – c/b can be written as
y = (b/a)x + y-intercept
Use (x1, y1) to find y-intercept
y1 = (b/a)x1 + y-intercept
y-intercept = y1– (b/a)x1
y = (b/a)x + y1– (b/a)x1
3) Set the two equations equal to each other to find expressions for the points of intersection (x2, y2)
Set y = (-a/b)x – c/b and y = (b/a)x + y1– (b/a)x1 equal to each other
(-a/b)x – c/b = (b/a)x + y1– (b/a)x1
(b/a)x + (a/b)x = -c/b + (b/a)x1 – y1
(b/a)x + (a/b)x = (ba/ba) × [(-c/b + (b/a)x1 – y1]
(b/a + a/b)x = (-ca + b2x1 – y1ba) / ba
[ (a2 + b2)/ab ] / x = (-ca + b2x1 – y1ba) / ba
x = (-ca + b2x1 – y1ba) / a2 + b2 ( this is x2 )
Now, let us find y2 using the equation y = (-a/b)x – c/b
(-a/b)x = -a/b[ (-ca + b2x1 – bay1) / (a2 + b2) ]
(-a/b)x = (ca2 – ab2x1 + ba2y1) / b(a2 + b2)
(-a/b)x – c/b = [(ca2 – ab2x1 + ba2y1) / b(a2 + b2)] – c/b
(-a/b)x – c/b = (ca2 – ab2x1 + ba2y1 – ca2 – b2c) / b(a2 + b2)
(-a/b)x – c/b = (- ab2x1 + ba2y1 – b2c) / b(a2 + b2)
(-a/b)x – c/b = b[(- abx1 + a2y1 – bc)] / b(a2 + b2)
(-a/b)x – c/b = (- abx1 + a2y1 – bc) / (a2 + b2)
y = (- abx1 + a2y1 – bc) / (a2 + b2) (this is y2)
To summarize,
x2 = (-ca + b2x1 – y1ba) / a2 + b2
y2 = (- abx1 + a2y1 – bc) / (a2 + b2)
Now, find the distance between a point and a line using (x1,y1) and (x2,y2)
d=√(x2−x1)2+(y2−y1)2�=(�2−�1)2+(�2−�1)2
d=√(−ca+b2x1−y1baa2+b2−x1)2+(−bc+a2y1−abx1a2+b2−y1)2�=(−��+�2�1−�1���2+�2−�1)2+(−��+�2�1−���1�2+�2−�1)2
d=√(−ca+b2x1−y1ba−a2x1−b2x1a2+b2)2+(−bc+a2y1−abx1−a2y1−b2y1a2+b2)2�=(−��+�2�1−�1��−�2�1−�2�1�2+�2)2+(−��+�2�1−���1−�2�1−�2�1�2+�2)2
d=√(−ca−y1ba−a2x1a2+b2)2+(−bc−abx1−b2y1a2+b2)2�=(−��−�1��−�2�1�2+�2)2+(−��−���1−�2�1�2+�2)2
d=√[−a(c+y1b+ax1)a2+b2]2+[−b(c+ax1+by1a2+b2]2�=[−�(�+�1�+��1)�2+�2]2+[−�(�+��1+��1�2+�2]2
d=√(−a)2(c+y1b+ax1)2(a2+b2)2+(−b)2(c+ax1+by1)2(a2+b2)2�=(−�)2(�+�1�+��1)2(�2+�2)2+(−�)2(�+��1+��1)2(�2+�2)2
d=√a2(c+y1b+ax1)2(a2+b2)2+b2(c+ax1+by1)2(a2+b2)2�=�2(�+�1�+��1)2(�2+�2)2+�2(�+��1+��1)2(�2+�2)2
d=√(a2+b2)(c+y1b+ax1)2(a2+b2)2�=(�2+�2)(�+�1�+��1)2(�2+�2)2
d=√(c+y1b+ax1)2(a2+b2)�=(�+�1�+��1)2(�2+�2)
d=|c+y1b+ax1|√a2+b2�=|�+�1�+��1|�2+�2
Leave a Reply