Common Lisp defines several kinds of numbers. The number data type includes various kinds of numbers supported by LISP.
The number types supported by LISP are −
- Integers
- Ratios
- Floating-point numbers
- Complex numbers
The following diagram shows the number hierarchy and various numeric data types available in LISP −
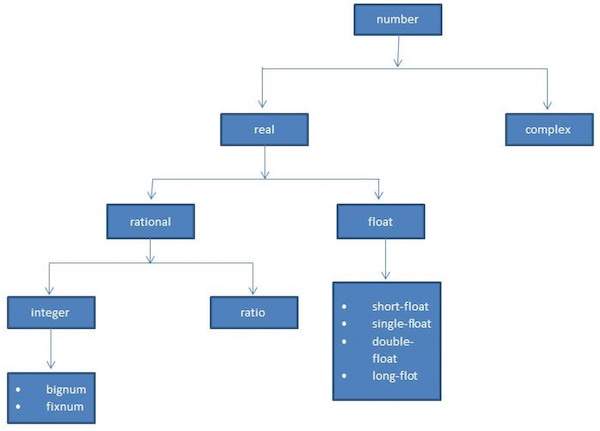
Various Numeric Types in LISP
The following table describes various number type data available in LISP −
| Sr.No. | Data type & Description |
|---|---|
| 1 | fixnumThis data type represents integers which are not too large and mostly in the range -215 to 215-1 (it is machine-dependent) |
| 2 | bignumThese are very large numbers with size limited by the amount of memory allocated for LISP, they are not fixnum numbers. |
| 3 | ratioRepresents the ratio of two numbers in the numerator/denominator form. The / function always produce the result in ratios, when its arguments are integers. |
| 4 | floatIt represents non-integer numbers. There are four float data types with increasing precision. |
| 5 | complexIt represents complex numbers, which are denoted by #c. The real and imaginary parts could be both either rational or floating point numbers. |
Example
Create a new source code file named main.lisp and type the following code in it.
(write (/ 1 2))
(terpri)
(write ( + (/ 1 2) (/ 3 4)))
(terpri)
(write ( + #c( 1 2) #c( 3 -4)))When you execute the code, it returns the following result −
1/2
5/4
#C(4 -2)
Number Functions
The following table describes some commonly used numeric functions −
| Sr.No. | Function & Description |
|---|---|
| 1 | +, -, *, /Respective arithmetic operations |
| 2 | sin, cos, tan, acos, asin, atanRespective trigonometric functions. |
| 3 | sinh, cosh, tanh, acosh, asinh, atanhRespective hyperbolic functions. |
| 4 | expExponentiation function. Calculates ex |
| 5 | exptExponentiation function, takes base and power both. |
| 6 | sqrtIt calculates the square root of a number. |
| 7 | logLogarithmic function. It one parameter is given, then it calculates its natural logarithm, otherwise the second parameter is used as base. |
| 8 | conjugateIt calculates the complex conjugate of a number. In case of a real number, it returns the number itself. |
| 9 | absIt returns the absolute value (or magnitude) of a number. |
| 10 | gcdIt calculates the greatest common divisor of the given numbers. |
| 11 | lcmIt calculates the least common multiple of the given numbers. |
| 12 | isqrtIt gives the greatest integer less than or equal to the exact square root of a given natural number. |
| 13 | floor, ceiling, truncate, roundAll these functions take two arguments as a number and returns the quotient; floor returns the largest integer that is not greater than ratio, ceiling chooses the smaller integer that is larger than ratio, truncate chooses the integer of the same sign as ratio with the largest absolute value that is less than absolute value of ratio, and round chooses an integer that is closest to ratio. |
| 14 | ffloor, fceiling, ftruncate, froundDoes the same as above, but returns the quotient as a floating point number. |
| 15 | mod, remReturns the remainder in a division operation. |
| 16 | floatConverts a real number to a floating point number. |
| 17 | rational, rationalizeConverts a real number to rational number. |
| 18 | numerator, denominatorReturns the respective parts of a rational number. |
| 19 | realpart, imagpartReturns the real and imaginary part of a complex number. |
Example
Create a new source code file named main.lisp and type the following code in it.
(write (/ 45 78))
(terpri)
(write (floor 45 78))
(terpri)
(write (/ 3456 75))
(terpri)
(write (floor 3456 75))
(terpri)
(write (ceiling 3456 75))
(terpri)
(write (truncate 3456 75))
(terpri)
(write (round 3456 75))
(terpri)
(write (ffloor 3456 75))
(terpri)
(write (fceiling 3456 75))
(terpri)
(write (ftruncate 3456 75))
(terpri)
(write (fround 3456 75))
(terpri)
(write (mod 3456 75))
(terpri)
(setq c (complex 6 7))
(write c)
(terpri)
(write (complex 5 -9))
(terpri)
(write (realpart c))
(terpri)
(write (imagpart c))When you execute the code, it returns the following result −
15/26
0
1152/25
46
47
46
46
46.0
47.0
46.0
46.0
6
#C(6 7)
#C(5 -9)
6
7
Leave a Reply