Are they any patterns or rules when adding, subtracting, multiplying or dividing even and odd numbers?
The following diagrams show some rules and examples when adding, subtracting, multiplying, or dividing even and odd numbers. The rules for division is only true if the quotient is a whole number. Scroll down the page for more examples and explanations.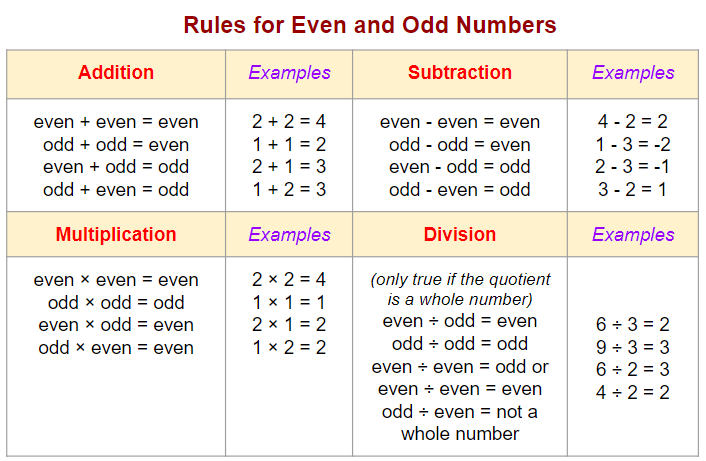
What are even numbers?
- A number that ends in a 0, 2, 4, 6 or 8.
- A number that is divisible by 2.
- A number that is a multiple of 2.
What are odd numbers?
- A number that ends in 1, 3, 5, 7 or 9.
- A number that is not divisible by 2.
- A number that is not a multiple of 2.
Using the properties of odd and even numbers – Addition
- Use addition with pairs of odd or even numbers or one odd and one even number.
- Use understanding of this relationship to check the accuracy of calculations.
Sum of two even numbers is always even. (even + even = even)
Sum of two odd numbers is always even. (odd + odd = even)
Sum of an even and odd number is odd. (even + odd = odd or odd + even = odd)
Using the properties of odd and even numbers – Subtraction
- Use subtraction with pairs of odd or even numbers or one odd and one even number.
- Use understanding of this relationship to check the accuracy of calculations.
When both numbers are even, the difference of the numbers is even. (even – even = even)
When both numbers are odd, the difference of the numbers is even. (odd – odd = even)
When one number is even and the other odd, the difference of the numbers is odd. (even – odd = odd or odd – even = odd)
Using the properties of odd and even numbers – Multiplication
- Use multiplication with pairs of odd or even numbers or one odd and one even number.
- Use understanding of this relationship to check the accuracy of calculations.
When both numbers are even, the product of the numbers is even. (even × even = even)
When both numbers are odd, the product of the numbers is odd. (odd × odd = odd)
When one number is even and the other odd, the product of the numbers is even. (even × odd = even or odd × even = even)
Using the properties of odd and even numbers – Division
- Use multiplication with pairs of odd or even numbers or one odd and one even number.
- Use understanding of this relationship to check the accuracy of calculations.
The following rules for division is only true if the quotient is a whole number.
even ÷ odd = even
odd ÷ odd = even
even ÷ even = odd or even
odd ÷ even = not a whole number
Prime Numbers and Composite Numbers
In this lesson, we will learn
- prime numbers
- composite numbers
- why 1 is not a prime number
What is a Prime Number?
A prime number is a whole number that has exactly two factors, 1 and itself.
For example
The number 29 has exactly two factors, which are 1 and 29.
So, 29 is a prime number.
The prime numbers up to 100 are
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97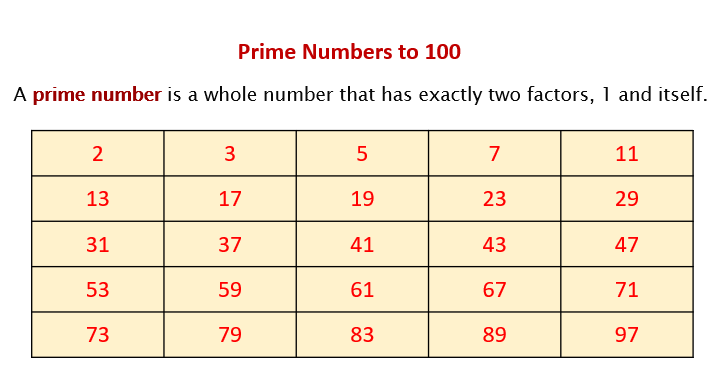
We can use the Sieve of Eratosthenes to find all prime numbers up to any given limit.
The number 2 is the only prime that is even. All other even numbers have 2 as a factor and so they are composite numbers.
Twin primes are pairs of primes whose difference is 2.
(3, 5), (5, 7) and (11, 13) are examples of twin primes.
What is a Composite Number?
A number that has more than 2 factors is called a composite number.
For example:
The number 28 has six factors which are 1, 2, 4, 7, 14, and 28.
So, 28 is not a prime number. It is a composite numbers.
Example:
Determine whether each of the following number is prime.
a) 43
b) 57
Solution:
a) 43 is only divisible by 1 and 43. It is a prime number.
b) 57 ÷ 3 = 19. It is not a prime number.
What are relatively prime numbers?
When two composite numbers have no common factors (other than 1), they are said to be relatively prime. For example, the numbers 8 and 15 are relatively prime.
How to identify prime numbers?
How to distinguish between prime numbers and composite numbers?
A prime number is a number greater than 1, which is only divisible by 1 and itself.
Recognizing prime and composite numbers
Example:
Determine whether the following numbers are prime, composite or neither:
24, 2, 1, 17
Is 1 a prime number?
No, the number 1 is not a prime number because it has only one factor.
Another reason is related to the Fundamental Theorem of Arithmetic as explained in the following video.
Leave a Reply