A prime number is a whole number that has exactly two factors, 1 and itself.
The Sieve of Eratosthenes is an ancient algorithm that can help us find all prime numbers up to any given limit.
How does the Sieve of Eratosthenes work?
The following example illustrates how the Sieve of Eratosthenes can be used to find all the prime numbers that are less than 100.
Step 1: Write the numbers 1 to 100 in ten rows.
Step 2: Cross out 1 because 1 is not a prime.
Step 3: Circle 2 and cross out all multiples of 2. (2, 4, 6, 8, 10, …)
Step 4: Circle 3 and cross out all multiples of 3. (3, 6, 9, 12, 15, …)
Step 5: Circle 5 and cross out all multiples of 5. (5, 10, 15, 20, …)
Step 6: Circle 7 and cross out all multiples of 7. (7, 14, 21, 28, …)
Circle all the numbers that are not crossed out and they are the prime numbers less than 100.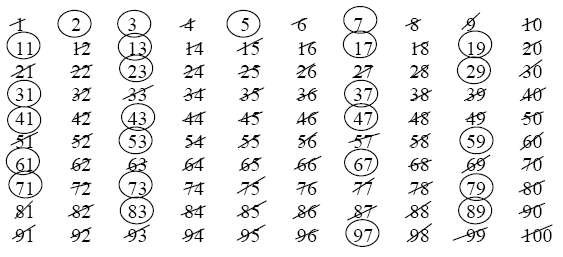
How to use the Sieve of Eratosthenes to find all the prime numbers less than 100?
The Sieve of Eratosthenes is a simple, ancient algorithm for finding all prime numbers up to a specified integer. In this case we are using a chart up to 100.
Signed Operations
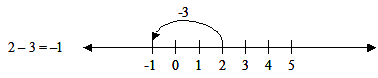
On the number line, moving to the right is positive.
On the number line, moving to the left is negative.
Simplifying Signed Operations
Remember these rules for paired signs when you need to do signed operations:
+
+
+ ++
+
For example:
+ ( 3) = 3
(+ 3) = 3
+ (+ 3) = +3
( 3) = +3
Number Properties
In these lessons, we will learn three basic number properties (or laws) that apply to arithmetic operations: Commutative Property, Associative Property and Distributive Property.
Summary of Number Properties
The following table gives a summary of the commutative, associative and distributive properties. Scroll down the page for more examples and explanations of the number properties.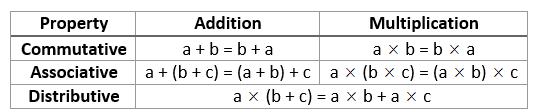
Commutative Property
An operation is commutative if a change in the order of the numbers does not change the results. This means the numbers can be swapped.
Numbers can be added in any order.
For example:
4 + 5 = 5 + 4
x + y = y + x
Numbers can be multiplied in any order.
For example:
5 × 3 = 3 × 5
a × b = b × a
Numbers that are subtracted are NOT commutative.
For example:
4 – 5 ≠ 5 – 4
x – y ≠ y –x
Numbers that are divided are NOT commutative.
For example:
4 ÷ 5 ≠ 5 ÷ 4
x ÷ y ≠ y ÷ x
Associative Property
An operation is associative if a change in grouping does not change the results. This means the parenthesis (or brackets) can be moved.
Numbers that are added can be grouped in any order.
For example:
(4 + 5) + 6 = 5 + (4 + 6)
(x + y) + z = x + (y + z)
Numbers that are multiplied can be grouped in any order.
For example:
(4 × 5) × 6 = 5 × (4 × 6)
(x × y) × z = x × (y × z)
Numbers that are subtracted are NOT associative.
For example:
(4 – 5) – 6 ≠ 4 – (5– 6)
x – y) – z ≠ x – (y – z)
Numbers that are divided are NOT associative.
For example:
(4 ÷ 5) ÷ 6 ≠ 4 ÷ (5÷ 6)
(x ÷ y ) ÷ z ≠ x ÷ ( y ÷ z)
Distributive Property
Distributive property allows you to remove the parenthesis (or brackets) in an expression. Multiply the value outside the brackets with each of the terms in the brackets.
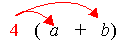
For example:
4(a + b) = 4a + 4b
7(2c – 3d + 5) = 14c – 21d + 35
What happens if you need to multiply (a – 3)(b + 4)?
You do the same thing but with one value at a time.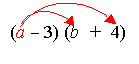
For example:
Multiply a with each term to get a × b + 4 × a = ab + 4a
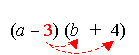
Then, multiply 3 with each term to get “ –3b – 12” (take note of the sign operations).
Put the two results together to get “ab + 4a – 3b – 12”
Therefore, (a – 3)(b + 4) = ab + 4a – 3b – 12
The Commutative Property of addition and multiplication.
The addition of real numbers is commutative.
The multiplication of real numbers is commutative.
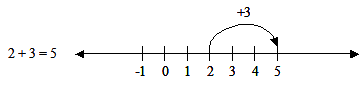
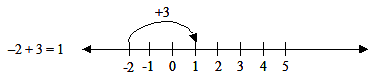
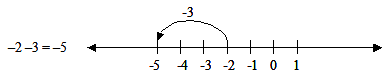
Leave a Reply