In these lessons, we learn what the commutative property means and how to use it in arithmetic operations.
The basic Number Properties (or laws) that apply to arithmetic operations are Commutative Property, Associative Property, Identity Property and Distributive Property.
The following diagrams show the Commutative Property of Addition and Multiplication. Scroll down the page for more examples and solutions.
Commutative Property
An operation is commutative if a change in the order of the numbers does not change the results. This means the numbers can be swapped.
Numbers can be added in any order.
For example:
4 + 5 = 5 + 4
x + y = y + x
Numbers can be multiplied in any order.
For example:
5 × 3 = 3 × 5
a × b = b × a
Numbers that are subtracted are NOT commutative.
For example:
4 – 5 ≠ 5 – 4
x – y ≠ y –x
Numbers that are divided are NOT commutative.
For example:
4 ÷ 5 ≠ 5 ÷ 4
x ÷ y ≠ y ÷ x
Associative & Identity Property
The basic Number Properties (or laws) that apply to arithmetic operations are Commutative Property, Associative Property, Identity Property and Distributive Property. In these lessons, we will learn the associative property and identity property of numbers.
Summary Of Number Properties
The following table summarizes the number properties for addition and multiplication: Commutative, Associative and Identity. Scroll down the page for more examples, explanations and solutions.
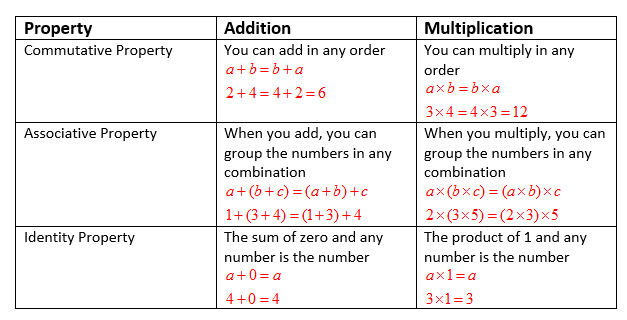
Associative Property
The associative property states that the sum or product of a set of numbers is the same, no matter how the numbers are grouped.
An operation is associative if a change in grouping does not change the results. This means the parenthesis (or brackets) can be moved.
Numbers that are added can be grouped in any order.
| For example: | (4 + 5) + 6 = 5 + (4 + 6) |
| (x + y) + z = x + (y + z) |
Numbers that are multiplied can be grouped in any order.
| For example: | (4 × 5) × 6 = 5 × (4 × 6) |
| (x × y) × z = x × (y × z) |
Numbers that are subtracted are NOT associative.
| For example: | (4 – 5) – 6 ≠ 5 – (4 – 6) |
| (x – y) – z ≠ x – (y – z) |
Numbers that are divided are NOT associative.
| For example: | (4 ÷ 5) ÷ 6 ≠ 5 ÷ (4 ÷ 6) |
| (x ÷ y ) ÷ z ≠ y ÷ ( x ÷ z) |
What is the Associative Property?
The following video explains: What is the associative property? Why does it have the name it does? How can you recognize it when you see it? How can you distinguish it from other situations that look very similar?
The Associative Property
This video explains the associative property and how it can be used.
The following video shows an example on the Associative Property of Addition.
The following video shows an example of the Associative Property of Multiplication.
Identity Properties
Identity Property (or Zero Property) of Addition
When you add 0 to any a number, the sum is that number.
For example: 325 + 0 = 325.
Identity Property (or One Property) of Multiplication
When you multiply any number by 1, the product is that number.
For example: 65, 148 × 1 = 65, 148
Zero Property of Multiplication
The product of any number and 0 is 0
For example: 874 × 0 = 0
Identity Property of Addition & Multiplication
Identity Property
The basic Number Properties (or laws) that apply to arithmetic operations are Commutative Property, Associative Property, Identity Property and Distributive Property.
https://classroom.google.com/sharewidget?usegapi=1&size=32&url=https%3A%2F%2Fwww.onlinemathlearning.com%2Fidentity-property.html&origin=https%3A%2F%2Fwww.onlinemathlearning.com&gsrc=3p&ic=1&jsh=m%3B%2F_%2Fscs%2Fabc-static%2F_%2Fjs%2Fk%3Dgapi.lb.en.y0xCMa4KeeI.O%2Fd%3D1%2Frs%3DAHpOoo8-3MGCaatZB3kdS5TpZdd-gOSBHg%2Fm%3D__features__#_methods=onPlusOne%2C_ready%2C_close%2C_open%2C_resizeMe%2C_renderstart%2Concircled%2Cdrefresh%2Cerefresh&id=I0_1708009976650&_gfid=I0_1708009976650&parent=https%3A%2F%2Fwww.onlinemathlearning.com&pfname=&rpctoken=17894445
Share this page to Google Classroom
Related Pages
Identity Property Of Addition, Multiplication
More Lessons On Numbers
Math Worksheets
The following table gives the commutative property, associative property and identity property for addition and subtraction. Scroll down the page for more examples and solutions of the number properties.
Identity Properties
Identity Property (Or Zero Property) Of Addition
When you add 0 to any number, the sum is that number.
For example: 325 + 0 = 325.
Identity Property (Or One Property) Of Multiplication
When you multiply any number by 1, the product is that number.
For example: 65,148 × 1 = 65,148
Zero Property Of Multiplication
The product of any number and 0 is 0.
For example: 874 × 0 = 0
Identity Property Of Addition & Multiplication
Identity Property of Addition: Any number plus zero is the original number.
Identity Property of Multiplication: Any number times one is the original number.
Zero is the identity number of addition and one is the identity number of multiplication.
Identity Property Of Addition And Multiplication
Identity Property of addition states that any number plus zero is the original number.
Identity property of multiplication states any number times one is the original number.
Identity Property
This video defines the Identity Property.
The Identity Property is made up of two parts: Additive Identity and Multiplicative Identity.
The Additive Identity is
Add zero (0) to a number, the sum is that number.
The Multiplicative Identity is
Multiply a number by 1, the Product is that number.
Divide a number by itself, the Quotient is 1.
Commutative And Zero Properties Of Multiplication
Commutative, Associative And Identity Properties
Example:
- Tell which property is represented
a) (2 ˙ 6) ˙ 1 = 2 ˙ (6 ˙ 1)
b) 3 + 0 = 3
c) 7 + 9 = 9 + 7 - Simplify each expression. Justify each step.
a) 17 + 14 + 3
b) 12 ˙ 3 ˙ 5
c) 21 + 16 + 9
Leave a Reply