In these lessons, we will learn what are perfect squares and how to calculate the square root of a perfect square.

What Is The Square Of A Number?

The square of a number means to multiply the number by itself.

Example:
The square of 3 is 3 × 3 = 9

The square of a number can be written in exponent notation such as 3² where 3 is base and 2 is the exponent.

3² is read as “three to the second power” or “three squared”.

What Are Perfect Squares?

Perfect squares are the squares of whole numbers.

Example:
1, 4, 9, 16, 25 and 36 are the first 6 perfect squares because
1² = 1 × 1 = 1
2² = 2 × 2 = 4
3² = 3 × 3 = 9
4² = 4 × 4 = 16
5² = 5 × 5 = 25
6² = 6 × 6 = 36

How To Check For Perfect Squares?

We use repeated division by prime factors to check whether a given number is a perfect square.

Example:
Check whether 441 is a perfect square.

Solution:

441 = 3 × 3 × 7 × 7
  = 3 × 7 × 3 × 7
  = 21 × 21
  = 21²

So, 441 is a perfect square.

How To Determine If A Number Is A Perfect Square?

We can use prime factorization to check if a number is a perfect square.

How To Find Smallest Positive Whole Number That Is A Perfect Square And A Multiple Of A Specific Whole Number?

Examples:

1. What is the smallest positive whole number that is a perfect square and is a multiple of 24?
2. What is the smallest positive whole number that is a perfect square and is a multiple of 150?

How To Find The Square Of Negative Numbers, Decimals And Fractions?

We can also have the square of negative numbers, decimals and fractions.

When calculating the square of a number, take note of the following:

1. The square of a number is always positive.
   Example:
   (−5)² = (−5) × (−5) = 25
   (−7)² = (−7) × (−7) = 49

Observe two important properties of a square in the last example above:
a) The square of a negative number becomes a positive number.
b) The square of a signed number is the same as the square of the unsigned number, i.e. (−7)² = 49 = 7².

2. The square of a decimal will have twice the number of decimal places as the original decimal.
   Example:
   (0.3)² = 0.3 × 0.3 = 0.09 ( 1 d.p. after squaring becomes 2 d.p.)
   (0.03)² = 0.03 × 0.03 = 0.0009 ( 2 d.p. after squaring become 4 d.p.)
   10.2² = 10.2 × 10.2 = 104.04 ( 1 d.p. after squaring becomes 2 d.p.)
3. To square a fraction, multiply the numerator by itself and do the same for the denominator.
   Example: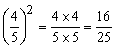
   
   

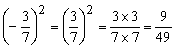
Take note that if a positive fraction which is less than 1 is squared, the result is always smaller than the original fraction.

4. To square a mixed number, change it to an improper fraction before calculating the square.
   Example: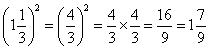
   

Squaring Negative Numbers

Look for parentheses to group negative numbers that are to be squared.

Example:
Simplify (−3)² and −3²

Square Roots

In this lesson, we will look at how to find the square roots of perfect squares and the square roots of non-perfect squares.

Square Roots Of Perfect Squares

The opposite of squaring a number is finding the square root.

We know that 4 squared = 4² = 16. The square root of 16 is the number that can be multiplied by itself to get 16, which is 4.

The symbol used for square root is . (The symbol is also called the radical sign)
 = 4 (The square root of 16 is 4).

Notice that –4 is also a square root of 16.
Check: (–4) × (–4) = 16, i.e. (–4)² = 16.

We see that the number 16 has two square roots: a positive square root and a negative square root.

For any positive value x, 

We can get the square root of perfect squares in the following way:

Example :

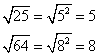
Similarly, for any positive value x, 

Example :

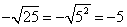
Also, take note that

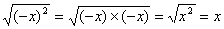
Example:

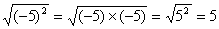
Example:

Work out the following:

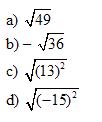
Solution:

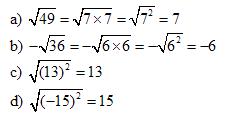
The following video shows how to find the square root of perfect squares.

Square Roots Of Non-Perfect Squares

Square root of numbers that are not perfect squares would be an irrational number. (Irrational numbers are numbers that cannot be written as fractions. and in decimal form, these numbers go on forever and the same pattern of digits is not repeated.)

For example, = 1.4142…

Usually, we would need to use a calculator to get the square root of a non-perfect square.

Squares & Square Roots

What are squares and square roots?

Squares are a simple form of exponents. The square of a number is the number multiplied by itself, for example:

4 × 4 = 16

It is also written as: 

The square root of a number is the inverse of the square.

Thus, , because 4 × 4 =16

Also, note that , because (4) × (4) =16

We write (  means + and -)

It would be helpful that you know the squares of integers up to 12:

x	1	2	3	4	5	6	7	8	9	10	11	12
x2	1	4	9	16	25	36	49	64	81	100	121	144

And also the square roots:

x	1	4	9	16	25	36	49	64	81	100	121	144
	1	2	3	4	5	6	7	8	9	10	11	12

To square a fraction, multiply the numerator by itself and do the same for the denominator.

Example:

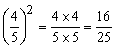
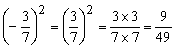
Take note that if a positive fraction which is less than 1 is squared, the result is always smaller than the original fraction.

Simplifying Square Roots (or Radicals)

In these lessons we will look into two methods that can be used to simplify square roots (or radicals): the perfect square method and the prime factorization method.

The following examples show how to simplify square roots: Find Perfect Square, Find Prime Factors. Scroll down the page for examples and solutions.

Simplify square roots using the perfect square method

The steps involved are:

1. Find the perfect square(s) that will divide the number in the square root.
2. Write the number as a factor of the perfect square(s).
3. Reduce the perfect squares.

Example:
Simplify 

Solution:
Step 1: The perfect square 16 divides 48

Step 2: Write 48 as a factor of 16

48 = 16 × 3

Step 3: Reduce square root of 16

How to simplify square roots using the perfect square method?
The following video shows more examples of simplifying square roots using the perfect square method. The perfect square method is suitable for small numbers for example less than 1000. For bigger numbers the prime factorization method may be better.

It would be useful for you to memorize the first five perfect squares of prime numbers.
1² = 1, 2² = 4, 3²= 9, 5² = 25, 7² = 49, 11² = 121

Step 1: Factor out the perfect squares
Step 2: Separate perfect squares using product of square roots property
Step 3: Simplify

Examples:
Simplify the following square roots:
a) square root of 72
b) square root of 288
c) square root of 108

How to simplify square roots by factoring out perfect squares?

Example:
Simplify the following square roots:
a) square root of 60
b) square root of 108

Simplify square roots using the prime factorization method

The steps involved are:

1. Break the number in the square root into prime factors
2. For each pair of factors, “take one out” of the square root sign
3. The remaining factors in the square root sign are multiplied together.

Example:
Simplify 

Solution:

Step 1. Break the number 12 into prime factors
12 = 2 × 2 × 3

Step 2: Take 2 out of the square root sign

Example:
Simplify 

Solution:

Step 1. Break the number 90 into prime factors

90 = 2 × 3 × 3 × 5

Step 2: Take 3 out of the square root sign

Step 3: Multiply 2 and 5

How to simplifying square roots using the prime factorization method?
The following video shows more examples of simplifying square roots using the prime factorization method.
Step 1: Factor into product of primes
Step 2: Circle the pairs of factors
Step 3: Remove the pairs and multiply by each number removed.

Example:
Simplify the following square roots:
a) square root of 18
b) square root of 420

Examples of simplifying square roots using the prime factorization.

Example:
Simplify the following square roots:
a) square root of 180
b) square root of 200

How to use prime factorization to simplify square roots?

Example:
Simplify the following square roots:
a) square root of 84
b) square root of 392

How to Simplify Square Roots With Fractions?
How to deal with square roots in the denominator of a fraction.

Example:
Simplify the following square roots:
a) \(\sqrt {\frac{7}{3}} \)
b) \(\sqrt {\frac{24}{5}} \)

Simplifying Radicals

What are radicals?

A radical is the indicated root of a quantity.

For example

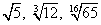
The radical sign is the symbol 

Some radicals have exact values.

For example

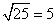
Some radicals do not have exact values

For example

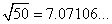
How to simplify radicals?

Sometimes, we may want to simplify the radicals.

For example

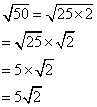
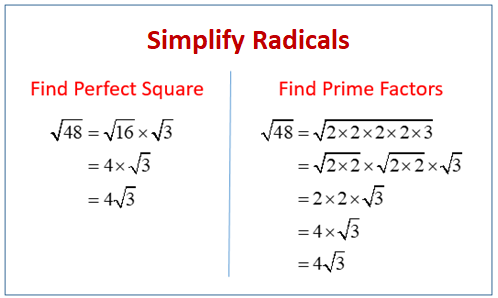
The following diagram shows some examples of simplify radicals using the perfect square method and the prime factors method. Scroll down the page for more examples and solutions for simplifying radicals.

Simplify Squares Roots (Radicals) That Have Fractions

In these lessons, we will look at some examples of simplifying fractions within a square root (or radical). Some techniques used are: find the square root of the numerator and denominator separately, reduce the fraction and change to improper fraction.

Separate Numerator & Denominator

A. The square root of some fractions can be determined by finding the square root of the numerator and denominator separately.

Example:
1625−−√=16√25√=42√52√=451625=1625=4252=45

For any positive number x and y,
xy−−√=x√y√��=��

In other words, the square root of a fraction is a fraction of square roots.

Reduce Fraction

B. Some fractions can be reduced to fractions with perfect squares as the numerator and denominator. Then, the square root of the simplified fraction can be determined as shown in the example below.

Example:
1850−−√=925−−√=32√52√=351850=925=3252=35

Change to Improper Fraction

C. For a mixed number, change it to an improper fraction before finding the square root.

Example:
11336−−−√=4936−−√=72√62√=76=11611336=4936=7262=76=116

Example:
Calculate the value of each of the following:
a)2536−−√b)1832−−√c)11125−−−√a)2536b)1832c)11125

Solution:

How to simplify fractions inside a square root?

How to simplify square roots in the denominator of a fraction?

Square Roots of Fractions/Rational Numbers

Finding the square of rational numbers for perfect squares as well as estimating non-perfect squares.

Quotient Rule & Simplifying Square Roots

An introduction to the quotient rule for square roots and radicals and how to use it to simplify expressions containing radicals.

Multiplying Square Roots (or Radicals)

In these lessons, we will look at how to multiply square roots (radicals) of whole numbers, decimals and fractions.

The following table shows the Multiplication Property of Square Roots. Scroll down the page for examples and solutions on how to multiply square roots.

A. When a square root of a given number is multiplied by itself, the result is the given number.

 for any positive number x.

Example:

Evaluate

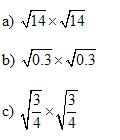
Solution:

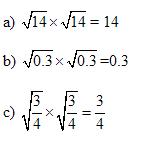
B . Product of two square roots of two positive numbers a and b is equal to the square root of product ab,

 for any positive numbers a and b.

Example:

Evaluate

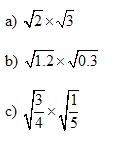
Solution: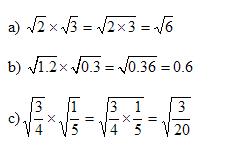

Examples of multiplying square roots or radicals and using prime factorization to simplify