Two Dimensional Tensor

Two-dimensional tensor is similar to the two-dimensional metrics. A two-dimensional metrics have n number of rows and n number of columns. Similarly, two-dimensional tensor has n rows and n columns also.

A two-dimensional tensor has the following representation

A gray scalar image is a two-dimensional matrix of pixels. Each pixel’s intensity denoted by a numeric value that ranges from 0 to 255 such that intensity value of 0 indicates no intensity something being completely black and 255 representing of maximum intensity something being completely white. We can store this two-dimensional grid of values.

Creating two-dimensional tensor

For creating a two-dimensional tensor, you have first to create a one-dimensional tensor using arrange () method of the torch. This method contains two parameters of integer type. This method arranges the elements in tensor as per the given parameters. Once your one-dimensional tensor is created, then our next step is to change its view in two-dimensional form and store this view in the two-dimensional type of variable.

Let see an example of creating a two dimensional tensor

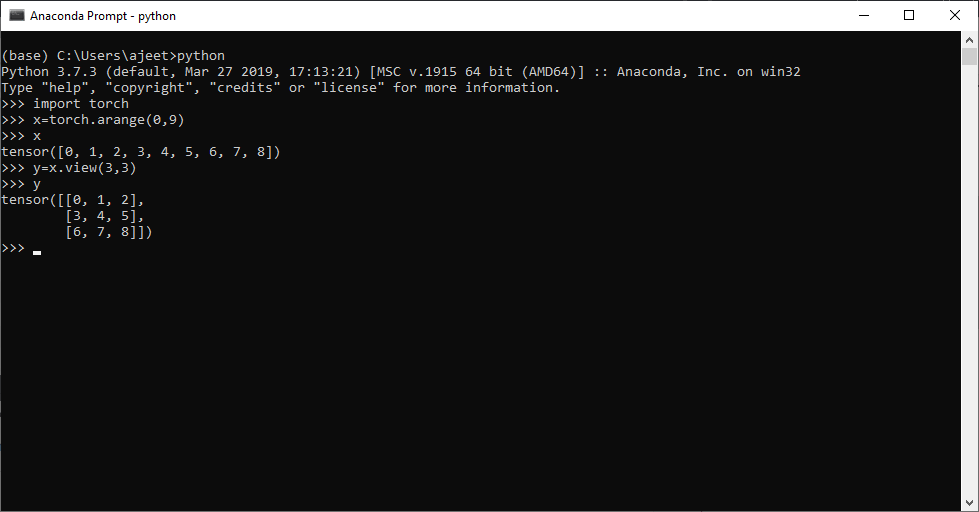
import torch  

x=torch.arange(0,9)  

x  

y=x.view(3,3)  

y

Output:tensor([0, 1, 2, 3, 4, 5, 6, 7, 8]) tensor([[0, 1, 2], [3, 4, 5], [6, 7, 8]])

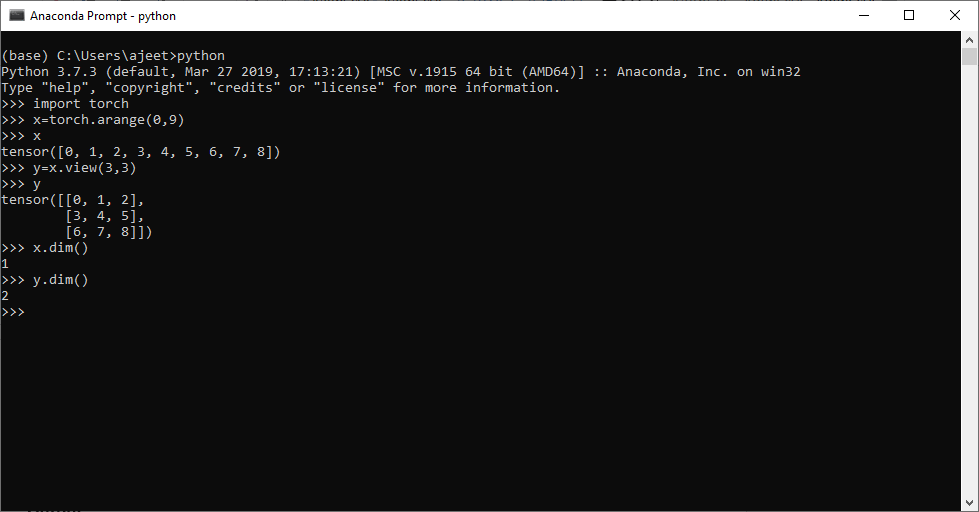
Note: To check the dimension of tensor we have to use dim() method of tensor.

import torch  



x=torch.arange(0,9)  



x  



y=x.view(3,3)  



y  



x.dim()  



y.dim()  

Output:tensor([0, 1, 2, 3, 4, 5, 6, 7, 8]) tensor([[0, 1, 2], [3, 4, 5], [6, 7, 8]]) 1 2

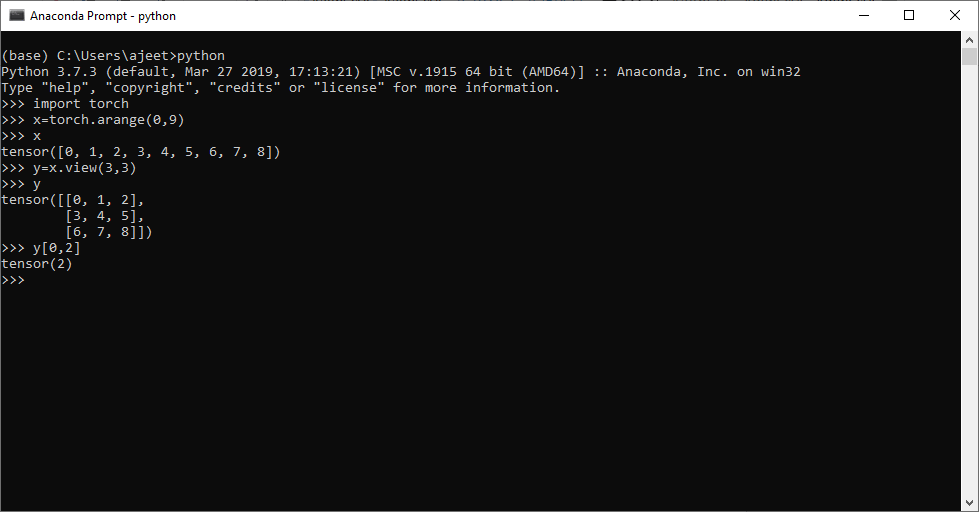
Accessing two-dimensional tensor elements

Let see an example of two-dimensional tensor to understand how to access a particular element from two-dimensional tensor using index.

Example

import torch  

x=torch.arange(0,9)  

x  

y=x.view(3,3)  

y  

y[0,2]

Output:tensor([0, 1, 2, 3, 4, 5, 6, 7, 8]) tensor([[0, 1, 2], [3, 4, 5], [6, 7, 8]]) tensor(2)

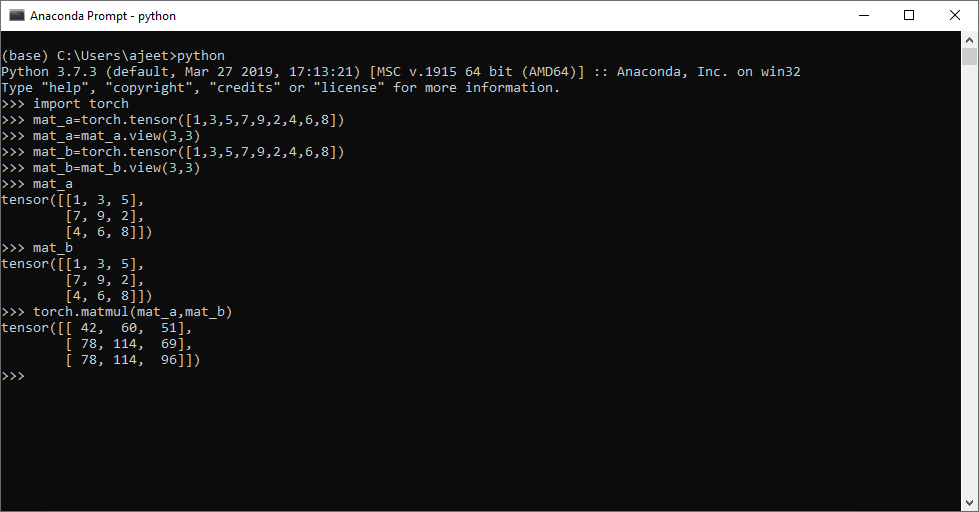
Tensors Multiplication

The multiplication is done in the same manner as metrics multiplication. Tensor multiplication is done with multiplying corresponding row with the corresponding column. Tensor multiplication plays a vital role in the deep learning model. Tensors can be one dimensional, two dimensional, three dimensional, and so on. Multiplication of tensor is done only with compatible size.

Let see an example of Tensor Multiplication

import torch  

mat_a=torch.tensor([1,3,5,7,9,2,4,6,8])  

mat_a=mat_a.view(3,3)  

mat_b=torch.tensor([1,3,5,7,9,2,4,6,8])  

mat_b=mat_b.view(3,3)  

mat_a  

mat_b  

torch.matmul(mat_a,mat_b)# We can also usemat_a @ mat_b

Output:tensor([[1, 3, 5], [7, 9, 2], [4, 6, 8]]) tensor([[1, 3, 5], [7, 9, 2], [4, 6, 8]]) tensor([[ 42, 60, 51], [ 78, 114, 69], [ 78, 114, 96]])

Three Dimensional Tensor

Three-dimensional tensor is made with the help of view () method. A three-dimensional tensor has the following structure

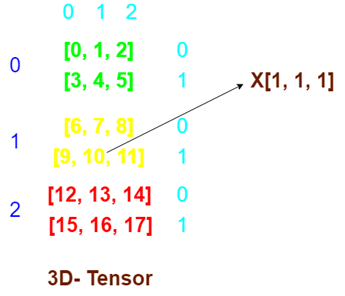
Accessing element from 3D- Tensor

Accessing elements from the 3D-tensor is quite easy. It will be done using the index.

Example

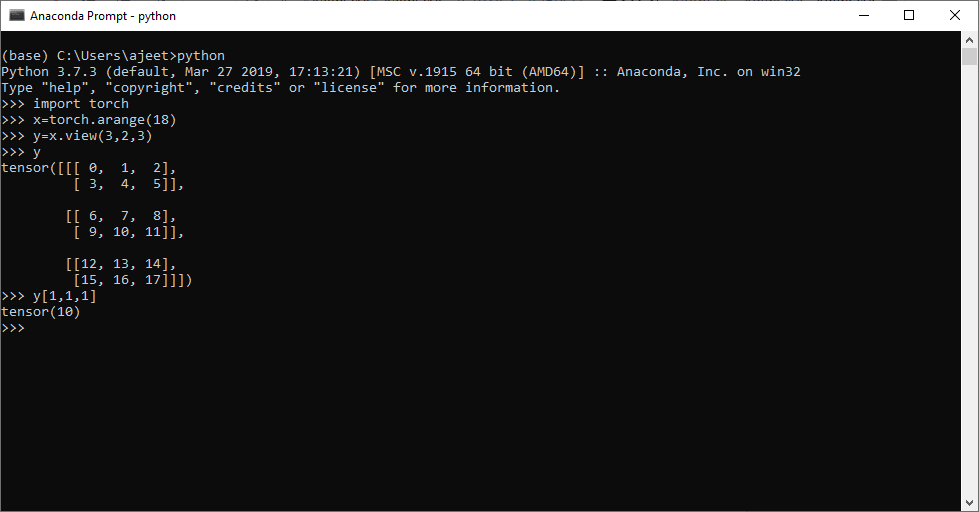
import torch  

x=torch.arange(18)  

y=x.view(3, 2, 3)  

y  

y[1,1,1]

Output:tensor([[[ 0, 1, 2], [ 3, 4, 5]], [[ 6, 7, 8], [ 9, 10, 11]], [[12, 13, 14], [15, 16, 17]]]) tensor(10)

Slicing of three-dimensional tensor

Segment slices are very similar to how we would slice a one-dimensional tensor. Slicing a tensor means to slice the elements of a tensor into a new tensor, or we can say slicing is a process of creating a new tensor by dividing a tensor.

Example

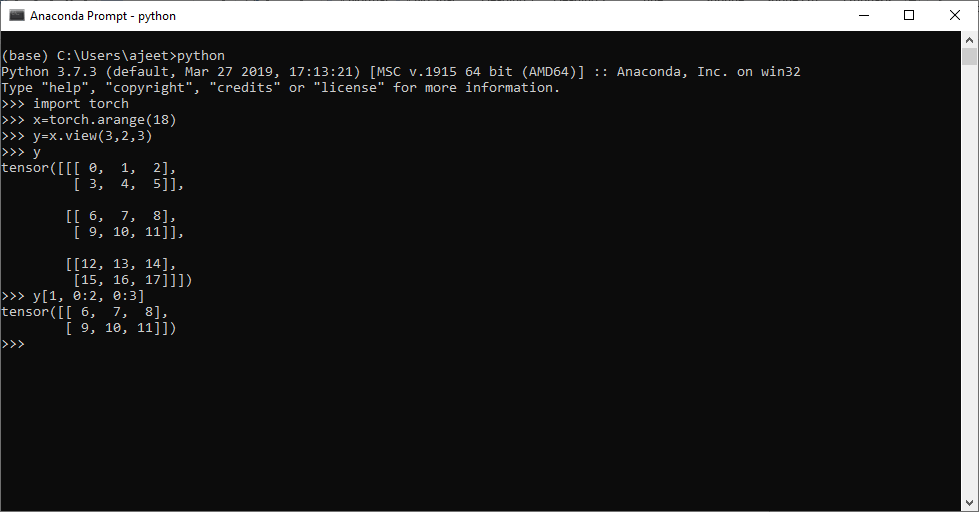
Let we have a three dimensional tensor which contains elements from 0 to 17 and we want to slice the tensor from 6 to 11.

import torch  

x=torch.arange(18)  

y=x.view(3,2,3)  

y  

y[1, 0:2, 0:3]      # can also apply y[1, :, :]

Output:tensor([[[ 0, 1, 2], [ 3, 4, 5]], [[ 6, 7, 8], [ 9, 10, 11]], [[12, 13, 14], [15, 16, 17]]]) tensor([[ 6, 7, 8], [ 9, 10, 11]])