Introduction
Let us consider the acute, the right and the obtuse angles as follows. If we close the third sides of these angles, acute, right and the obtuse triangles are formed. These triangles always have at least two acute triangles. The third angle decides the type of triangle. If the third angle is acute it is acute triangle; if the third angle is right angle, it is a right triangle; if the third angle is obtuse angle, the triangle is an obtuse triangle.
A triangle can have at most one right angle and at most one obtuse angle.Definitions
Triangles are polygons that always have 3 sides and 3 angles.
Triangles can be classified on the basis of their angles as acute, obtuse and right triangles.
An acute triangle has all of its angles as acute.
An obtuse triangle has one obtuse angle.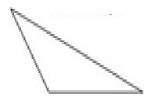
A right triangle has one right angle.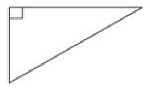 Example 1:
Example 1:
Identify the given triangle as acute, obtuse or right triangle.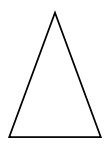
Solution
Step 1:
All angles of the given triangle are acute.
Step 2:
So the given triangle is an acute triangle.Example 2:
Identify the given triangle as acute, obtuse or right triangle.
Solution
Step 1:
One of the angles of the given triangle is a right angle.
Step 2:
So the given triangle is a right triangle.
Leave a Reply